如图,反比例函数 y= 与一次函数 y= k 2 x+ b的图象交于 A(2,4), B(﹣4, m)两点.
(1)求 k 1, k 2, b的值;
(2)求△ AOB的面积;
(3)若 M( x 1, y 1), N( x 2, y 2)是反比例函数 y= 的图象上的两点,且 x 1< x 2, y 1< y 2,指出点 M、 N各位于哪个象限.

如图,反比例函数
的图象与直线 交于点
交于点 ,
, ,其两边分别与两坐标轴的正半轴交于点
,其两边分别与两坐标轴的正半轴交于点 ,
, ,四边形
,四边形 的面积为6.
的面积为6.
(1)求 的值;
的值;
(2)点 在反比例函数
的图象上,若点
在反比例函数
的图象上,若点 的横坐标为3,
的横坐标为3, ,其两边分别与
,其两边分别与 轴的正半轴,直线
轴的正半轴,直线 交于点
交于点 ,
, ,问是否存在点
,问是否存在点 ,使得
,使得 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

如图,在平面直角坐标系 中,反比例函数 的图象经过点 ,点 在 轴的负半轴上, 交 轴于点 , 为线段 的中点.
(1) ,点 的坐标为 ;
(2)若点 为线段 上的一个动点,过点 作 轴,交反比例函数图象于点 ,求 面积的最大值.

如图,已知 , ,反比例函数 的图象过点 ,反比例函数 的图象过点 .
(1)求 和 的值;
(2)过点 作 轴,与双曲线 交于点 .求 的面积.

如图,已知反比例函数 的图象和一次函数 的图象都过点 ,过点 作 轴的垂线,垂足为 , 为坐标原点, 的面积为1.
(1)求反比例函数和一次函数的解析式;
(2)设反比例函数图象与一次函数图象的另一交点为 ,过 作 轴的垂线,垂足为 ,求五边形 的面积.
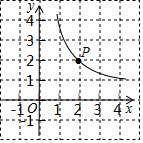
如图,反比例函数 的图象过格点(网格线的交点) .
(1)求反比例函数的解析式;
(2)在图中用直尺和 铅笔画出两个矩形(不写画法),要求每个矩形均需满足下列两个条件:
①四个顶点均在格点上,且其中两个顶点分别是点 ,点 ;
②矩形的面积等于 的值.
小明在研究矩形面积 与矩形的边长 , 之间的关系时,得到下表数据:
|
|
0.5 |
1 |
1.5 |
2 |
3 |
4 |
6 |
12 |
|
|
12 |
6 |
4 |
3 |
2 |
|
1 |
0.5 |
结果发现一个数据被墨水涂黑了
(1)被墨水涂黑的数据为 .
(2) 与 之间的函数关系式为 ,且 随 的增大而 .
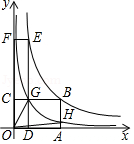
(3)如图是小明画出的 关于 的函数图象,点 、 均在该函数的图象上,其中矩形 的面积记为 ,矩形 的面积记为 ,请判断 和 的大小关系,并说明理由.
(4)在(3)的条件下, 交 于点 ,反比例函数 的图象经过点 交 于点 ,连接 、 ,则四边形 的面积为 .
试题篮
()