小明在研究矩形面积 与矩形的边长 , 之间的关系时,得到下表数据:
|
|
0.5 |
1 |
1.5 |
2 |
3 |
4 |
6 |
12 |
|
|
12 |
6 |
4 |
3 |
2 |
|
1 |
0.5 |
结果发现一个数据被墨水涂黑了
(1)被墨水涂黑的数据为 .
(2) 与 之间的函数关系式为 ,且 随 的增大而 .
(3)如图是小明画出的 关于 的函数图象,点 、 均在该函数的图象上,其中矩形 的面积记为 ,矩形 的面积记为 ,请判断 和 的大小关系,并说明理由.
(4)在(3)的条件下, 交 于点 ,反比例函数 的图象经过点 交 于点 ,连接 、 ,则四边形 的面积为 .
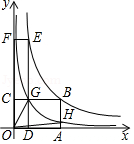
如图,过反比例函数 的图象上一点 作 轴于点 ,连接 ,若 ,则 的值为

| A. |
2 |
B. |
3 |
C. |
4 |
D. |
5 |
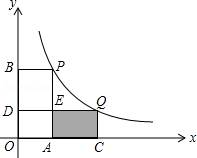
如图,在平面直角坐标系中,点 、 在函数 的图象上,当 时,过点 分别作 轴、 轴的垂线,垂足为点 , ;过点 分别作 轴、 轴的垂线,垂足为点 、 . 交 于点 ,随着 的增大,四边形 的面积
| A. |
减小 |
B. |
增大 |
C. |
先减小后增大 |
D. |
先增大后减小 |
如图,在x轴正半轴上依次截取OA1=A1A2=A2A…An-1An(n为正整数),过点A1、A2、A3、…、An分别作x轴的垂线,与反比例函数y=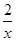 (x>0)交于点P1、P2、P3、…、Pn,连接P1P2、P2P3、…、Pn-1Pn,过点P2、P3、…、Pn分别向P1A1、P2A2、…、Pn-1An-1作垂线段,构成的一系列直角三角形(见图中阴影部分)的面积和是 ()
(x>0)交于点P1、P2、P3、…、Pn,连接P1P2、P2P3、…、Pn-1Pn,过点P2、P3、…、Pn分别向P1A1、P2A2、…、Pn-1An-1作垂线段,构成的一系列直角三角形(见图中阴影部分)的面积和是 ()
A. |
B.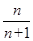 |
C. |
D.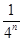 |
在反比例函数 的图象上,有一系列点
的图象上,有一系列点 ,若
,若 的横坐标为2,且以后每点的横坐标与它前一个点的横坐标的差都为2,现分别过点
的横坐标为2,且以后每点的横坐标与它前一个点的横坐标的差都为2,现分别过点 ,作x轴与y轴的垂线段,构成若干个矩形如下图所示,将图中阴影部分的面积从左到右依次记为
,作x轴与y轴的垂线段,构成若干个矩形如下图所示,将图中阴影部分的面积从左到右依次记为 ,则
,则 ______.(用n的代数式表示)
______.(用n的代数式表示)
如图,直线 和双曲线y=
和双曲线y= (
( )交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、OP,设△AOC的面积为
)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、OP,设△AOC的面积为 ,△BOD的面积为
,△BOD的面积为 ,△POE的面积为
,△POE的面积为 ,则()
,则()
A. B.
B.
C. D.
D.
(年新疆乌鲁木齐市)如图,在直角坐标系xOy中,点A,B分别在x轴和y轴, .∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数
.∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数 的图象过点C.当以CD为边的正方形的面积为
的图象过点C.当以CD为边的正方形的面积为 时,k的值是()
时,k的值是()
A.2 B.3 C.5 D.7
如图,点B1在反比例函数y= (x>0)的图象上,过点B1分别作x轴和y轴的垂线,垂足为C1和A,得到第一个矩形AOC1B1,点C1的坐标为(1,0);取x轴上一点C2(
(x>0)的图象上,过点B1分别作x轴和y轴的垂线,垂足为C1和A,得到第一个矩形AOC1B1,点C1的坐标为(1,0);取x轴上一点C2( ,0),过点C2作x轴的垂线交反比例函数图象于点B2,过B2作线段B2 A1⊥B1C1,,交B1C1于点A1,得到第二个矩形A1C1C2B2;依次在x轴上取点C3(2,0),C4(
,0),过点C2作x轴的垂线交反比例函数图象于点B2,过B2作线段B2 A1⊥B1C1,,交B1C1于点A1,得到第二个矩形A1C1C2B2;依次在x轴上取点C3(2,0),C4( ,0) 按此规律作矩形,则第10个矩形A9C9C10B10的面积为 .
,0) 按此规律作矩形,则第10个矩形A9C9C10B10的面积为 .
试题篮
()