如图,一次函数 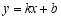 与反比例函数
交于
与反比例函数
交于  ,
, 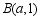 ,与
,与 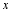 轴,
轴, 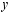 轴分别交于点
轴分别交于点 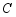 ,
, 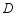 .
.
(1)直接写出一次函数 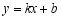 的表达式和反比例函数
的表达式;
的表达式和反比例函数
的表达式;
(2)求证:  .
.
已知反比例函数 与一次函数y=x+2的图象交于点A(﹣3,m)
(1)求反比例函数的解析式;
(2)如果点M的横、纵坐标都是不大于3的正整数,求点M在反比例函数图象上的概率.
如图,一次函数y=ax+b(a≠0)的图象与反比例函数 的图象交于A(﹣3,2),B(2,n).
(1)求反比例函数 的解析式;
(2)求一次函数y=ax+b的解析式;
(3)观察图象,直接写出不等式 的解集.

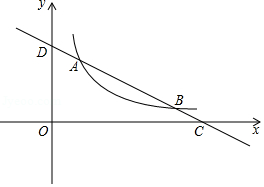
如图,已知一次函数 的图象与反比例函数 的图象交于点A(﹣1,2)和点B,点C在y轴上.
(1)当△ABC的周长最小时,求点C的坐标;
(2)当 x+b<
x+b< 时,请直接写出x的取值范围.
时,请直接写出x的取值范围.

△ABC的顶点坐标为A(﹣2,3)、B(﹣3,1)、C(﹣1,2),以坐标原点O为旋转中心,顺时针旋转90°,得到△A′B′C′,点B′、C′分别是点B、C的对应点.
(1)求过点B′的反比例函数解析式;
(2)求线段CC′的长.

如图,一次函数 的图象分别与反比例函数 的图象在第一象限交于点 ,与 轴的负半轴交于点 ,且 .
(1)求函数 和 的表达式;
(2)已知点 ,试在该一次函数图象上确定一点 ,使得 ,求此时点 的坐标.

如图, 、 两点的坐标分别为 , ,将线段 绕点 逆时针旋转 得到线段 ,过点 作 ,垂足为 ,反比例函数 的图象经过点 .
(1)直接写出点 的坐标,并求反比例函数的解析式;
(2)点 在反比例函数 的图象上,当 的面积为3时,求点 的坐标.

如图,在平面直角坐标系中,一次函数 的图象与 轴, 轴的交点分别为点 ,点 ,与反比例函数 的图象交于 , 两点, 轴于点 ,连接 , .
(1)求反比例函数的解析式;
(2)求 的面积.

已知反比例函数 的图象经过点 .
(1)求 的值.
(2)完成下面的解答.
解不等式组
解:解不等式①,得 .
根据函数 的图象,得不等式②的解集 .
把不等式①和②的解集在数轴上表示出来.

从图中可以找出两个不等式解集的公共部分,得不等式组的解集 .
如图所示,的顶点
在反比例函数
的图象上,直线
交
轴于点
,且点
的纵坐标为5,过点
、
分别作
轴的垂线
、
,垂足分别为点
、
,且
.
(1)若点为线段
的中点,求
的值;
(2)若为等腰直角三角形,
,其面积小于3.
①求证:;
②把称为
,
,
,
两点间的“
距离”,记为
,求
,
,
的值.

如图,一次函数 的图象与反比例函数 为常数且 的图象相交于 , 两点.
(1)求反比例函数的表达式;
(2)将一次函数 的图象沿 轴向下平移 个单位 ,使平移后的图象与反比例函数 的图象有且只有一个交点,求 的值.

如图,在平面直角坐标系中,点 为坐标原点,菱形 的顶点 的坐标为 .
(1)求过点 的反比例函数 的解析式;
(2)连接 ,过点 作 交 轴于点 ,求直线 的解析式.

如图,反比例函数 和一次函数 的图象都经过点 和点 .
(1) , ;
(2)求一次函数的解析式,并直接写出 时 的取值范围;
(3)若点 是反比例函数 的图象上一点,过点 作 轴,垂足为 ,则 的面积为 .
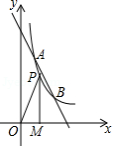
如图,直线 与反比例函数 的图象交于 , 两点,已知点 的坐标为 , 的面积为8.
(1)填空:反比例函数的关系式为 ;
(2)求直线 的函数关系式;
(3)动点 在 轴上运动,当线段 与 之差最大时,求点 的坐标.

试题篮
()