初中数学二次函数的应用试题

如图1，过点的抛物线与直线交于点．点是线段上一动点，过点作轴的垂线，垂足为点，交抛物线于点．设的面积为，点的横坐标为．

（1）请直接写出的值及抛物线的解析式．

（2）为探究最大时点的位置，甲、乙两同学结合图形给出如下解析：

甲：借助的长与三角形面积公式，求出关于的函数关系式，可确定点的位置．

乙：当点运动到点或点时，的值可看作0，则当点运动到中点时，最大，即最大时，点为的中点．

请参考甲的方法求出最大时点的坐标，进而判断乙的猜想是否正确，并说明理由．

（3）拓展探究：如图2，直线与任意抛物线相交于、两点，是线段上的一个动点，过点作抛物线对称轴的平行线，交该抛物线于点．当的面积最大时，点一定是线段的中点吗？试作出判断并说明理由．

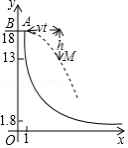
如图是轮滑场地的截面示意图，平台距轴（水平）18米，与轴交于点，与滑道交于点，且米．运动员（看成点）在方向获得速度米秒后，从处向右下飞向滑道，点是下落路线的某位置．忽略空气阻力，实验表明：，的竖直距离（米与飞出时间（秒的平方成正比，且时，，的水平距离是米．

（1）求，并用表示；

（2）设．用表示点的横坐标和纵坐标，并求与的关系式（不写的取值范围），及时运动员与正下方滑道的竖直距离；

（3）若运动员甲、乙同时从处飞出，速度分别是5米秒、米秒．当甲距轴1.8米，且乙位于甲右侧超过4.5米的位置时，直接写出的值及的范围．

某厂按用户的月需求量（件完成一种产品的生产，其中，每件的售价为18万元，每件的成本（万元）是基础价与浮动价的和，其中基础价保持不变，浮动价与月需求量（件成反比，经市场调研发现，月需求量与月份为整数，，符合关系式为常数），且得到了表中的数据．

月份（月	1	2
成本（万元件）	11	12
需求量（件月）	120	100

（1）求与满足的关系式，请说明一件产品的利润能否是12万元；

（2）求，并推断是否存在某个月既无盈利也不亏损；

（3）在这一年12个月中，若第个月和第个月的利润相差最大，求．