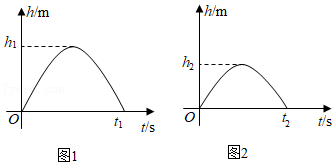
以初速度 (单位: 从地面竖直向上抛出小球,从抛出到落地的过程中,小球的高度 (单位: 与小球的运动时间 (单位: 之间的关系式是 .现将某弹性小球从地面竖直向上抛出,初速度为 ,经过时间 落回地面,运动过程中小球的最大高度为 (如图 ;小球落地后,竖直向上弹起,初速度为 ,经过时间 落回地面,运动过程中小球的最大高度为 (如图 .若 ,则 .
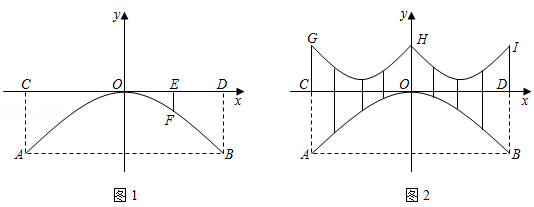
如图1是一座抛物线型拱桥侧面示意图.水面宽 与桥长 均为 ,在距离 点6米的 处,测得桥面到桥拱的距离 为 ,以桥拱顶点 为原点,桥面为 轴建立平面直角坐标系.
(1)求桥拱顶部 离水面的距离.
(2)如图2,桥面上方有3根高度均为 的支柱 , , ,过相邻两根支柱顶端的钢缆呈形状相同的抛物线,其最低点到桥面距离为 .
①求出其中一条钢缆抛物线的函数表达式.
②为庆祝节日,在钢缆和桥拱之间竖直装饰若干条彩带,求彩带长度的最小值.
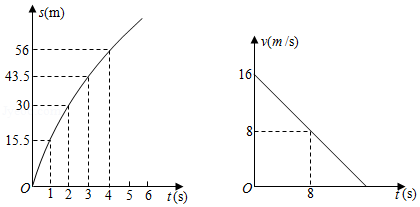
在平面直角坐标系中, 为原点, 是等腰直角三角形, , ,顶点 ,点 在第一象限,矩形 的顶点 , ,点 在 轴的正半轴上,点 在第二象限,射线 经过点 .
(Ⅰ)如图①,求点 的坐标;
(Ⅱ)将矩形 沿 轴向右平移,得到矩形 ,点 , , , 的对应点分别为 , , , .设 ,矩形 与 重叠部分的面积为 .
①如图②,当点 在 轴正半轴上,且矩形 与 重叠部分为四边形时, 与 相交于点 ,试用含有 的式子表示 ,并直接写出 的取值范围;
②当 时,求 的取值范围(直接写出结果即可).
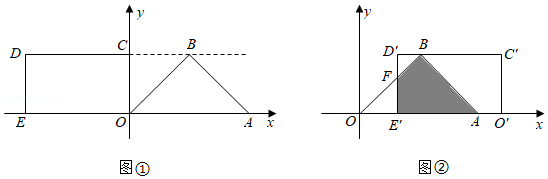
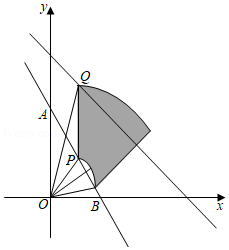
如图,直线 与坐标轴交于 、 两点,点 是线段 上的一个动点,过点 作 轴的平行线交直线 于点 , 绕点 顺时针旋转 ,边 扫过区域(阴影部分)面积的最大值是
| A. |
|
B. |
|
C. |
|
D. |
|
如图,已知点 ,点 为直线 上的一动点,点 , , 于点 ,连接 .若直线 与 正半轴所夹的锐角为 ,那么当 的值最大时, 的值为 .
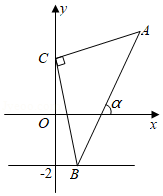
公路上正在行驶的甲车,发现前方 处沿同一方向行驶的乙车后,开始减速,减速后甲车行驶的路程 (单位: 、速度 (单位: 与时间 (单位: 的关系分别可以用二次函数和一次函数表示,其图象如图所示.
(1)当甲车减速至 时,它行驶的路程是多少?
(2)若乙车以 的速度匀速行驶,两车何时相距最近,最近距离是多少?
甲、乙两汽车出租公司均有50辆汽车对外出租,下面是两公司经理的一段对话:
| 甲公司经理:如果我公司每辆汽车月租费3000元,那么50辆汽车可以全部租出.如果每辆汽车的月租费每增加50元,那么将少租出1辆汽车.另外,公司为每辆租出的汽车支付月维护费200元. 乙公司经理:我公司每辆汽车月租费3500元,无论是否租出汽车,公司均需一次性支付月维护费共计1850元. |
说明:①汽车数量为整数;②月利润 月租车费 月维护费;③两公司月利润差 月利润较高公司的利润 月利润较低公司的利润.
在两公司租出的汽车数量相等的条件下,根据上述信息,解决下列问题:
(1)当每个公司租出的汽车为10辆时,甲公司的月利润是 48000 元;当每个公司租出的汽车为 辆时,两公司的月利润相等;
(2)求两公司月利润差的最大值;
(3)甲公司热心公益事业,每租出1辆汽车捐出 元 给慈善机构,如果捐款后甲公司剩余的月利润仍高于乙公司月利润,且当两公司租出的汽车均为17辆时,甲公司剩余的月利润与乙公司月利润之差最大,求 的取值范围.
在 中, , , ,点 是 所在平面内一点,则 取得最小值时,下列结论正确的是
| A. |
点 是 三边垂直平分线的交点 |
| B. |
点 是 三条内角平分线的交点 |
| C. |
点 是 三条高的交点 |
| D. |
点 是 三条中线的交点 |
如图,在矩形 中, , .动点 从点 出发沿折线 向终点 运动,在边 上以 的速度运动;在边 上以 的速度运动,过点 作线段 与射线 相交于点 ,且 ,连接 , .设点 的运动时间为 , 与 重合部分图形的面积为 .
(1)当点 与点 重合时,直接写出 的长;
(2)当点 在边 上运动时,直接写出 的长(用含 的代数式表示);
(3)求
关于
的函数解析式,并写出自变量
的取值范围.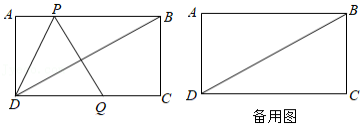
如图所示,在平面直角坐标系 中,一次函数 的图象 与函数 的图象(记为 交于点 ,过点 作 轴于点 ,且 ,点 在线段 上(不含端点),且 ,过点 作直线 轴,交 于点 ,交图象 于点 .
(1)求 的值,并且用含 的式子表示点 的横坐标;
(2)连接 、 、 ,记 、 的面积分别为 、 ,设 ,求 的最大值.

某超市从厂家购进 、 两种型号的水杯,两次购进水杯的情况如表:
| 进货批次 |
型水杯(个 |
型水杯(个 |
总费用(元 |
| 一 |
100 |
200 |
8000 |
| 二 |
200 |
300 |
13000 |
(1)求 、 两种型号的水杯进价各是多少元?
(2)在销售过程中, 型水杯因为物美价廉而更受消费者喜欢.为了增大 型水杯的销售量,超市决定对 型水杯进行降价销售,当销售价为44元时,每天可以售出20个,每降价1元,每天将多售出5个,请问超市应将 型水杯降价多少元时,每天售出 型水杯的利润达到最大?最大利润是多少?
(3)第三次进货用10000元钱购进这两种水杯,如果每销售出一个 型水杯可获利10元,售出一个 型水杯可获利9元,超市决定每售出一个 型水杯就为当地"新冠疫情防控"捐 元用于购买防控物资.若 、 两种型号的水杯在全部售出的情况下,捐款后所得的利润始终不变,此时 为多少?利润为多少?
如图, 的顶点坐标分别为 , , ,动点 、 同时从点 出发,分别沿 轴正方向和 轴正方向运动,速度分别为每秒3个单位和每秒2个单位,点 到达点 时点 、 同时停止运动.过点 作 分别交 、 于点 、 ,连接 、 .设运动时间为 (秒 .
(1)求点 的坐标(用含 的式子表示);
(2)求四边形 面积的最大值或最小值;
(3)是否存在这样的直线 ,总能平分四边形 的面积?如果存在,请求出直线 的解析式;如果不存在,请说明理由;
(4)连接 ,当 时,求点 到 的距离.

某商贸公司购进某种商品的成本为20元 ,经过市场调研发现,这种商品在未来40天的销售单价 (元 与时间 (天 之间的函数关系式为: ,且日销量 与时间 (天 之间的变化规律符合一次函数关系,如下表:
时间 (天 |
1 |
3 |
6 |
10 |
|
日销量 |
142 |
138 |
132 |
124 |
|
(1)填空: 与 的函数关系为 ;
(2)哪一天的销售利润最大?最大日销售利润是多少?
(3)在实际销售的前20天中,公司决定每销售 商品就捐赠 元利润 给当地福利院,后发现:在前20天中,每天扣除捐赠后的日销售利润随时间 的增大而增大,求 的取值范围.
某公司电商平台,在2021年五一长假期间,举行了商品打折促销活动,经市场调查发现,某种商品的周销售量 (件 是关于售价 (元 件)的一次函数,如表仅列出了该商品的售价 ,周销售量 ,周销售利润 (元 的三组对应值数据.
|
40 |
70 |
90 |
|
180 |
90 |
30 |
|
3600 |
4500 |
2100 |
(1)求 关于 的函数解析式(不要求写出自变量的取值范围);
(2)若该商品进价 (元 件),售价 为多少时,周销售利润 最大?并求出此时的最大利润;
(3)因疫情期间,该商品进价提高了 (元 件) ,公司为回馈消费者,规定该商品售价 不得超过55(元 件),且该商品在今后的销售中,周销售量与售价仍满足(1)中的函数关系,若周销售最大利润是4050元,求 的值.
红星公司销售一种成本为40元 件产品,若月销售单价不高于50元 件,一个月可售出5万件;月销售单价每涨价1元,月销售量就减少0.1万件.其中月销售单价不低于成本.设月销售单价为 (单位:元 件),月销售量为 (单位:万件).
(1)直接写出 与 之间的函数关系式,并写出自变量 的取值范围;
(2)当月销售单价是多少元时,月销售利润最大,最大利润是多少万元?
(3)为响应国家“乡村振兴”政策,该公司决定在某月每销售1件产品便向大别山区捐款 元.已知该公司捐款当月的月销售单价不高于70元 件,月销售最大利润是78万元,求 的值.
试题篮
()