初中数学二次函数的应用试题

某快递公司在甲地和乙地之间共设有29个服务驿站（包括甲站、乙站），一辆快递货车由甲站出发，依次途经各站驶往乙站，每停靠一站，均要卸下前面各站发往该站的货包各1个，又要装上该站发往后面各站的货包各1个．在整个行程中，快递货车装载的货包数量最多是　 　个．

结合西昌市创建文明城市要求，某小区业主委员会决定把一块长 $80m$，宽 $60m$的矩形空地建成花园小广场，设计方案如图所示，阴影区域为绿化区（四块绿化区为全等的直角三角形），空白区域为活动区，且四周出口宽度一样，其宽度不小于 $36m$，不大于 $44m$，预计活动区造价60元 $/m^2$，绿化区造价50元 $/m^2$，设绿化区域较长直角边为 $\mathit{xm}$．

（1）用含 $x$的代数式表示出口的宽度；

（2）求工程总造价 $y$与 $x$的函数关系式，并直接写出 $x$的取值范围；

（3）如果业主委员会投资28.4万元，能否完成全部工程？若能，请写出 $x$为整数的所有工程方案；若不能，请说明理由．

（4）业主委员会决定在（3）设计的方案中，按最省钱的一种方案，先对四个绿化区域进行绿化，在实际施工中，每天比原计划多绿化 $11m^2$，结果提前4天完成四个区域的绿化任务，问原计划每天绿化多少 $m^2$．

“绿水青山就是金山银山”的理念已融入人们的日常生活中，因此，越来越多的人喜欢骑自行车出行．某自行车店在销售某型号自行车时，以高出进价的 $50\%$标价．已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同．

（1）求该型号自行车的进价和标价分别是多少元？

（2）若该型号自行车的进价不变，按（1）中的标价出售，该店平均每月可售出51辆；若每辆自行车每降价20元，每月可多售出3辆，求该型号自行车降价多少元时，每月获利最大？最大利润是多少？

某水果商店销售一种进价为40元 $/$千克的优质水果，若售价为50元 $/$千克，则一个月可售出500千克；若售价在50元 $/$千克的基础上每涨价1元，则月销售量就减少10千克．

（1）当售价为55元 $/$千克时，每月销售水果多少千克？

（2）当月利润为8750元时，每千克水果售价为多少元？

（3）当每千克水果售价为多少元时，获得的月利润最大？

如图1，在平面直角坐标系中，直线 $\mathit{MN}$分别与 $x$轴、 $y$轴交于点 $M(6,0)$， $N(0$， $2\sqrt{3})$，等边 $\mathit{\Delta ABC}$的顶点 $B$与原点 $O$重合， $\mathit{BC}$边落在 $x$轴正半轴上，点 $A$恰好落在线段 $\mathit{MN}$上，将等边 $\mathit{\Delta ABC}$从图1的位置沿 $x$轴正方向以每秒1个单位长度的速度平移，边 $\mathit{AB}$， $\mathit{AC}$分别与线段 $\mathit{MN}$交于点 $E$， $F$（如图2所示），设 $\mathit{\Delta ABC}$平移的时间为 $t\left(s\right)$．

（1）等边 $\mathit{\Delta ABC}$的边长为　　；

（2）在运动过程中，当 $t=$　　时， $\mathit{MN}$垂直平分 $\mathit{AB}$；

（3）若在 $\mathit{\Delta ABC}$开始平移的同时．点 $P$从 $\mathit{\Delta ABC}$的顶点 $B$出发．以每秒2个单位长度的速度沿折线 $\mathit{BA}-\mathit{AC}$运动．当点 $P$运动到 $C$时即停止运动． $\mathit{\Delta ABC}$也随之停止平移．

①当点 $P$在线段 $\mathit{BA}$上运动时，若 $\mathit{\Delta PEF}$与 $\mathit{\Delta MNO}$相似．求 $t$的值；

②当点 $P$在线段 $\mathit{AC}$上运动时，设 $S_{\mathit{\Delta PEF}}=S$，求 $S$与 $t$的函数关系式，并求出 $S$的最大值及此时点 $P$的坐标．

我市雷雷服饰有限公司生产了一款夏季服装，通过实体商店和网上商店两种途径进行销售，销售一段时间后，该公司对这种商品的销售情况，进行了为期30天的跟踪调查，其中实体商店的日销售量 $y_1$（百件）与时间 $t(t$为整数，单位：天）的部分对应值如表所示，网上商店的日销售量 $y_2$（百件）与时间 $t(t$为整数，单位：天）的部分对应值如图所示．

时间 $t$（天 $)$	0	5	10	15	20	25	30
日销售量 $y_1$（百件）	0	25	40	45	40	25	0

（1）请你在一次函数、二次函数和反比例函数中，选择合适的函数能反映 $y_1$与 $t$的变化规律，并求出 $y_1$与 $t$的函数关系式及自变量 $t$的取值范围；

（2）求 $y_2$与 $t$的函数关系式，并写出自变量 $t$的取值范围；

（3）在跟踪调查的30天中，设实体商店和网上商店的日销售总量为 $y$（百件），求 $y$与 $t$的函数关系式；当 $t$为何值时，日销售总量 $y$达到最大，并求出此时的最大值．

如图，矩形 $\mathit{ABCD}$中， $\mathit{AB}=8\mathit{cm}$， $\mathit{BC}=6\mathit{cm}$，点 $P$从点 $A$出发，以 $1\mathit{cm}/s$的速度沿 $A\to D\to C$方向匀速运动，同时点 $Q$从点 $A$出发，以 $2\mathit{cm}/s$的速度沿 $A\to B\to C$方向匀速运动，当一个点到达点 $C$时，另一个点也随之停止．设运动时间为 $t\left(s\right)$， $\mathit{\Delta APQ}$的面积为 $S\left(c{m}^2\right)$，下列能大致反映 $S$与 $t$之间函数关系的图象是 $($　　 $)$

A．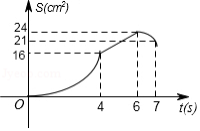

B．

C．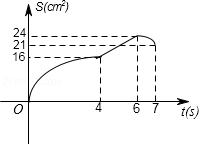

D．

如图1，排球场长为 $18m$，宽为 $9m$，网高为 $2.24m$，队员站在底线 $O$点处发球，球从点 $O$的正上方 $1.9m$的 $C$点发出，运动路线是抛物线的一部分，当球运动到最高点 $A$时，高度为 $2.88m$，即 $\mathit{BA}=2.88m$，这时水平距离 $\mathit{OB}=7m$，以直线 $\mathit{OB}$为 $x$轴，直线 $\mathit{OC}$为 $y$轴，建立平面直角坐标系，如图2．

（1）若球向正前方运动（即 $x$轴垂直于底线），求球运动的高度 $y\left(m\right)$与水平距离 $x\left(m\right)$之间的函数关系式（不必写出 $x$取值范围）．并判断这次发球能否过网？是否出界？说明理由．

（2）若球过网后的落点是对方场地①号位内的点 $P$（如图1，点 $P$距底线 $1m$，边线 $0.5m)$，问发球点 $O$在底线上的哪个位置？（参考数据： $\sqrt{2}$取 $1.4)$

超市销售某种儿童玩具，如果每件利润为40元（市场管理部门规定，该种玩具每件利润不能超过60元），每天可售出50件．根据市场调查发现，销售单价每增加2元，每天销售量会减少1件．设销售单价增加 $x$元，每天售出 $y$件．

（1）请写出 $y$与 $x$之间的函数表达式；

（2）当 $x$为多少时，超市每天销售这种玩具可获利润2250元？

（3）设超市每天销售这种玩具可获利 $w$元，当 $x$为多少时 $w$最大，最大值是多少？

某宾馆共有80间客房．宾馆负责人根据经验作出预测：今年7月份，每天的房间空闲数 $y$（间）与定价 $x$（元 $/$间）之间满足 $y=\frac{1}{4}x-42(x⩾168)$．若宾馆每天的日常运营成本为5000元，有客人入住的房间，宾馆每天每间另外还需支出28元的各种费用，宾馆想要获得最大利润，同时也想让客人得到实惠，应将房间定价确定为 $($　　 $)$

A．252元 $/$间B．256元 $/$间C．258元 $/$间D．260元 $/$间

飞机着陆后滑行的距离 $s$（单位：米）关于滑行的时间 $t$（单位：秒）的函数解析式是 $s=60t-\frac{3}{2}{t}^2$，则飞机着陆后滑行的最长时间为　    　秒．

随着龙虾节的火热举办，某龙虾养殖大户为了发挥技术优势，一次性收购了 $10000\mathit{kg}$小龙虾，计划养殖一段时间后再出售．已知每天养殖龙虾的成本相同，放养10天的总成本为166000，放养30天的总成本为178000元．设这批小龙虾放养 $t$天后的质量为 $\mathit{akg}$，销售单价为 $y$元 $/\mathit{kg}$，根据往年的行情预测， $a$与 $t$的函数关系为 $a=\left\{\begin{array}{c}10000(0⩽t⩽20)\\ 100t+8000(20<t⩽50)\end{array}\right.$， $y$与 $t$的函数关系如图所示．

（1）设每天的养殖成本为 $m$元，收购成本为 $n$元，求 $m$与 $n$的值；

（2）求 $y$与 $t$的函数关系式；

（3）如果将这批小龙虾放养 $t$天后一次性出售所得利润为 $W$元．问该龙虾养殖大户将这批小龙虾放养多少天后一次性出售所得利润最大？最大利润是多少？

（总成本 $=$放养总费用 $+$收购成本；利润 $=$销售总额 $-$总成本）

为迎接“世界华人炎帝故里寻根节”，某工厂接到一批纪念品生产订单，按要求在15天内完成，约定这批纪念品的出厂价为每件20元，设第 $x$天（ $1⩽x⩽15$，且 $x$为整数）每件产品的成本是 $p$元， $p$与 $x$之间符合一次函数关系，部分数据如表：

天数 $\left(x\right)$	1	3	6	10
每件成本 $p$（元）	7.5	8.5	10	12

任务完成后，统计发现工人李师傅第 $x$天生产的产品件数 $y$（件）与 $x$（天）满足如下关系： $y=\left\{\begin{array}{c}2x+20(1⩽x<10,且x\mathit{为整数})\\ 40\left(10⩽x⩽15,且x\mathit{为整数}\right)\end{array}\right.$

设李师傅第 $x$天创造的产品利润为 $W$元．

（1）直接写出 $p$与 $x$， $W$与 $x$之间的函数关系式，并注明自变量 $x$的取值范围：

（2）求李师傅第几天创造的利润最大？最大利润是多少元？

（3）任务完成后，统计发现平均每个工人每天创造的利润为299元．工厂制定如下奖励制度：如果一个工人某天创造的利润超过该平均值，则该工人当天可获得20元奖金．请计算李师傅共可获得多少元奖金？

小明家的洗手盆上装有一种抬启式水龙头（如图 $1)$，完全开启后，水流路线呈抛物线，把手端点 $A$，出水口 $B$和落水点 $C$恰好在同一直线上，点 $A$至出水管 $\mathit{BD}$的距离为 $12\mathit{cm}$，洗手盆及水龙头的相关数据如图2所示，现用高 $10.2\mathit{cm}$的圆柱型水杯去接水，若水流所在抛物线经过点 $D$和杯子上底面中心 $E$，则点 $E$到洗手盆内侧的距离 $\mathit{EH}$为　　 $\mathit{cm}$．

交通工程学理论把在单向道路上行驶的汽车看成连续的流体，并用流量、速度、密度三个概念描述车流的基本特征．其中流量 $q$（辆 $/$小时）指单位时间内通过道路指定断面的车辆数；速度 $v$（千米 $/$小时）指通过道路指定断面的车辆速度；密度 $k$（辆 $/$千米）指通过道路指定断面单位长度内的车辆数．

为配合大数据治堵行动，测得某路段流量 $q$与速度 $v$之间关系的部分数据如下表：

速度 $v$（千米 $/$小时）	$\dots$	5	10	20	32	40	48	$\dots$
流量 $q$（辆 $/$小时）	$\dots$	550	1000	1600	1792	1600	1152	$\dots$

（1）根据上表信息，下列三个函数关系式中，刻画 $q$， $v$关系最准确的是　　（只填上正确答案的序号）

① $q=90v+100$；② $q=\frac{32000}{v}$；③ $q=-2v^2+120v$．

（2）请利用（1）中选取的函数关系式分析，当该路段的车流速度为多少时，流量达到最大？最大流量是多少？

（3）已知 $q$， $v$， $k$满足 $q=\mathit{vk}$，请结合（1）中选取的函数关系式继续解决下列问题．

①市交通运行监控平台显示，当 $12⩽v<18$时道路出现轻度拥堵．试分析当车流密度 $k$在什么范围时，该路段将出现轻度拥堵；

②在理想状态下，假设前后两车车头之间的距离 $d$（米 $)$均相等，求流量 $q$最大时 $d$的值．