初中数学二次函数的应用试题

某品牌汽车销售店销售某种品牌的汽车，每辆汽车的进价16（万元）．当每辆售价为22（万元）时，每月可销售4辆汽车．根据市场行情，现在决定进行降价销售．通过市场调查得到了每辆降价的费用 $y_1$（万元）与月销售量 $x$（辆 $\left)\right(x⩾4)$满足某种函数关系的五组对应数据如下表：

$x$	4	5	6	7	8
$y_1$	0	0.5	1	1.5	2

（1）请你根据所给材料和初中所学的函数知识写出 $y_1$与 $x$的关系式 $y_1=$　　；

（2）每辆原售价为22万元，不考虑其它成本，降价后每月销售利润 $y=$（每辆原售价 $-y_1-$进价） $x$，请你根据上述条件，求出月销售量 $x(x⩾4)$为多少时，销售利润最大？最大利润是多少？

在“乡村振兴”行动中，某村办企业以 $A$， $B$两种农作物为原料开发了一种有机产品． $A$原料的单价是 $B$原料单价的1.5倍，若用900元收购 $A$原料会比用900元收购 $B$原料少 $100\mathit{kg}$．生产该产品每盒需要 $A$原料 $2\mathit{kg}$和 $B$原料 $4\mathit{kg}$，每盒还需其他成本9元．市场调查发现：该产品每盒的售价是60元时，每天可以销售500盒；每涨价1元，每天少销售10盒．

（1）求每盒产品的成本（成本 $=$原料费 $+$其他成本）；

（2）设每盒产品的售价是 $x$元 $(x$是整数），每天的利润是 $w$元，求 $w$关于 $x$的函数解析式（不需要写出自变量的取值范围）；

（3）若每盒产品的售价不超过 $a$元 $(a$是大于60的常数，且是整数），直接写出每天的最大利润．

端午节是我国入选世界非物质文化遗产的传统节日，端午节吃粽子是中华民族的传统习俗．市场上豆沙粽的进价比猪肉粽的进价每盒便宜10元，某商家用8000元购进的猪肉粽和用6000元购进的豆沙粽盒数相同．在销售中，该商家发现猪肉粽每盒售价50元时，每天可售出100盒；每盒售价提高1元时，每天少售出2盒．

（1）求猪肉粽和豆沙粽每盒的进价；

（2）设猪肉粽每盒售价 $x$元 $(50⩽x⩽65)$， $y$表示该商家每天销售猪肉粽的利润（单位：元），求 $y$关于 $x$的函数解析式并求最大利润．

为了实施乡村振兴战略，帮助农民增加收入，市政府大力扶持农户发展种植业，每亩土地每年发放种植补贴120元．张远村老张计划明年承租部分土地种植某种经济作物．考虑各种因素，预计明年每亩土地种植该作物的成本 $y$（元 $)$与种植面积 $x$（亩 $)$之间满足一次函数关系，且当 $x=160$时， $y=840$；当 $x=190$时， $y=960$．

（1）求 $y$与 $x$之间的函数关系式（不求自变量的取值范围）；

（2）受区域位置的限制，老张承租土地的面积不得超过240亩．若老张明年销售该作物每亩的销售额能达到2160元，当种植面积为多少时，老张明年种植该作物的总利润最大？最大利润是多少？

（每亩种植利润 $=$每亩销售额 $-$每亩种植成本 $+$每亩种植补贴）

某快餐店销售 $A$、 $B$两种快餐，每份利润分别为12元、8元，每天卖出份数分别为40份、80份．该店为了增加利润，准备降低每份 $A$种快餐的利润，同时提高每份 $B$种快餐的利润．售卖时发现，在一定范围内，每份 $A$种快餐利润每降1元可多卖2份，每份 $B$种快餐利润每提高1元就少卖2份．如果这两种快餐每天销售总份数不变，那么这两种快餐一天的总利润最多是　　元．

如今我国的大棚（如图 $1)$种植技术已十分成熟．小明家的菜地上有一个长为16米的蔬菜大棚，其横截面顶部为抛物线型，大棚的一端固定在离地面高1米的墙体 $A$处，另一端固定在离地面高2米的墙体 $B$处，现对其横截面建立如图2所示的平面直角坐标系．已知大棚上某处离地面的高度 $y$（米 $)$与其离墙体 $A$的水平距离 $x$（米 $)$之间的关系满足 $y=-\frac{1}{6}{x}^2+\mathit{bx}+c$，现测得 $A$， $B$两墙体之间的水平距离为6米．

（1）直接写出 $b$， $c$的值；

（2）求大棚的最高处到地面的距离；

（3）小明的爸爸欲在大棚内种植黄瓜，需搭建高为 $\frac{37}{24}$米的竹竿支架若干，已知大棚内可以搭建支架的土地平均每平方米需要4根竹竿，则共需要准备多少根竹竿？

从喷水池喷头喷出的水珠，在空中形成一条抛物线，如图所示，在抛物线各个位置上，水珠的竖直高度 $y$（单位： $m)$与它距离喷头的水平距离 $x$（单位： $m)$之间满足函数关系式 $y=-2x^2+4x+1$喷出水珠的最大高度是 　　 $m$．

某网店销售一款市场上畅销的蒸蛋器，进价为每个40元，在销售过程中发现，这款蒸蛋器销售单价为60元时，每星期卖出100个．如果调整销售单价，每涨价1元，每星期少卖出2个，现网店决定提价销售，设销售单价为 $x$元，每星期销售量为 $y$个．

（1）请直接写出 $y$（个 $)$与 $x$（元 $)$之间的函数关系式；

（2）当销售单价是多少元时，该网店每星期的销售利润是2400元？

（3）当销售单价是多少元时，该网店每星期的销售利润最大？最大利润是多少元？

我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式，此公式与古希腊几何学家海伦提出的公式如出一辙，即三角形的三边长分别为 $a$ ， $b$ ， $c$ ，记 $p=\frac{a+b+c}{2}$ ，则其面积 $S=\sqrt{p(p-a)(p-b)(p-c)}$ ．这个公式也被称为海伦 $-$ 秦九韶公式．若 $p=5$ ， $c=4$ ，则此三角形面积的最大值为 $($ 　　 $)$

A．

$\sqrt{5}$

B．

4

C．

$2\sqrt{5}$

D．

5

某药店选购了一批消毒液，进价为每瓶10元，在销售过程中发现，每天销售量 $y$（瓶 $)$与每瓶售价 $x$（元 $)$之间存在一次函数关系（其中 $10⩽x⩽21$，且 $x$为整数）．当每瓶消毒液售价为12元时，每天销售量为90瓶；当每瓶消毒液售价为15元时，每天销售量为75瓶．

（1）求 $y$与 $x$之间的函数关系式；

（2）设该药店销售该消毒液每天的销售利润为 $w$元，当每瓶消毒液售价为多少元时，药店销售该消毒液每天销售利润最大，最大利润是多少元？

某游乐场的圆形喷水池中心 $O$ 有一雕塑 $\mathit{OA}$ ，从 $A$ 点向四周喷水，喷出的水柱为抛物线，且形状相同．如图，以水平方向为 $x$ 轴，点 $O$ 为原点建立直角坐标系，点 $A$ 在 $y$ 轴上， $x$ 轴上的点 $C$ ， $D$ 为水柱的落水点，水柱所在抛物线（第一象限部分）的函数表达式为 $y=-\frac{1}{6}{(x-5)}^2+6$ ．

（1）求雕塑高 $\mathit{OA}$ ．

（2）求落水点 $C$ ， $D$ 之间的距离．

（3）若需要在 $\mathit{OD}$ 上的点 $E$ 处竖立雕塑 $\mathit{EF}$ ， $\mathit{OE}=10m$ ， $\mathit{EF}=1.8m$ ， $\mathit{EF}\perp \mathit{OD}$ ．问：顶部 $F$ 是否会碰到水柱？请通过计算说明．

某服装店以每件30元的价格购进一批 $T$恤，如果以每件40元出售，那么一个月内能售出300件，根据以往销售经验，销售单价每提高1元，销售量就会减少10件，设 $T$恤的销售单价提高 $x$元．

（1）服装店希望一个月内销售该种 $T$恤能获得利润3360元，并且尽可能减少库存，问 $T$恤的销售单价应提高多少元？

（2）当销售单价定为多少元时，该服装店一个月内销售这种 $T$恤获得的利润最大？最大利润是多少元？

今年以来，我市接待的游客人数逐月增加，据统计，游玩某景区的游客人数三月份为4万人，五月份为5.76万人．

（1）求四月和五月这两个月中该景区游客人数平均每月增长百分之几；

（2）若该景区仅有 $A$ ， $B$ 两个景点，售票处出示的三种购票方式如下表所示：

购票方式	甲	乙	丙
可游玩景点	$A$	$B$	$A$ 和     $B$
门票价格	100元     $/$ 人	80元     $/$ 人	160元     $/$ 人

据预测，六月份选择甲、乙、丙三种购票方式的人数分别有2万、3万和2万，并且当甲、乙两种门票价格不变时，丙种门票价格每下降1元，将有600人原计划购买甲种门票的游客和400人原计划购买乙种门票的游客改为购买丙种门票．

①若丙种门票价格下降10元，求景区六月份的门票总收入；

②问：将丙种门票价格下降多少元时，景区六月份的门票总收入有最大值？最大值是多少万元？

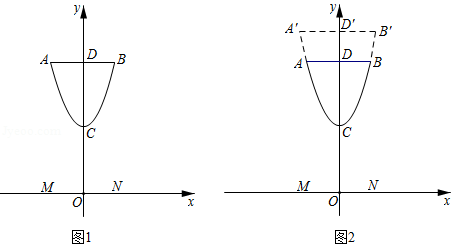
小聪设计奖杯，从抛物线形状上获得灵感，在平面直角坐标系中画出截面示意图，如图1，杯体 $\mathit{ACB}$ 是抛物线的一部分，抛物线的顶点 $C$ 在 $y$ 轴上，杯口直径 $\mathit{AB}=4$ ，且点 $A$ ， $B$ 关于 $y$ 轴对称，杯脚高 $\mathit{CO}=4$ ，杯高 $\mathit{DO}=8$ ，杯底 $\mathit{MN}$ 在 $x$ 轴上．

（1）求杯体 $\mathit{ACB}$ 所在抛物线的函数表达式（不必写出 $x$ 的取值范围）；

（2）为使奖杯更加美观，小敏提出了改进方案，如图2，杯体 $A\text{'}\mathit{CB}\text{'}$ 所在抛物线形状不变，杯口直径 $A\text{'}B\text{'}//\mathit{AB}$ ，杯脚高 $\mathit{CO}$ 不变，杯深 $\mathit{CD}\text{'}$ 与杯高 $\mathit{OD}\text{'}$ 之比为0.6，求 $A\text{'}B\text{'}$ 的长．

渠县是全国优质黄花主产地，某加工厂加工黄花的成本为30元 $/$千克，根据市场调查发现，批发价定为48元 $/$千克时，每天可销售500千克，为增大市场占有率，在保证盈利的情况下，工厂采取降价措施，批发价每千克降低1元，每天销量可增加50千克．

（1）写出工厂每天的利润 $W$元与降价 $x$元之间的函数关系．当降价2元时，工厂每天的利润为多少元？

（2）当降价多少元时，工厂每天的利润最大，最大为多少元？

（3）若工厂每天的利润要达到9750元，并让利于民，则定价应为多少元？