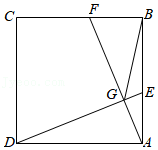
如图,在正方形 中, , 为边 上一点, 为边 上一点.连接 和 交于点 ,连接 .若 ,则 的最小值为 .
我们知道,两点之间线段最短,因此,连接两点间线段的长度叫做两点间的距离;同理,连接直线外一点与直线上各点的所有线段中,垂线段最短,因此,直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.类似地,连接曲线外一点与曲线上各点的所有线段中,最短线段的长度,叫做点到曲线的距离.依此定义,如图,在平面直角坐标系中,点 到以原点为圆心,以1为半径的圆的距离为 .

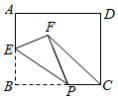
如图,在矩形 中, 为 的中点, 为 边上的任意一点,把 沿 折叠,得到 ,连接 .若 , ,则 的最小值为 .
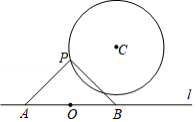
如图,已知 的半径为3,圆外一定点 满足 ,点 为 上一动点,经过点 的直线 上有两点 、 ,且 , , 不经过点 ,则 的最小值为 .
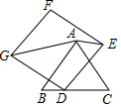
如图, 是等边三角形,点 为 边上一点, ,以点 为顶点作正方形 ,且 ,连接 , .若将正方形 绕点 旋转一周,当 取最小值时, 的长为 .
如图,在矩形 中, , , 是 边的中点, 是 边上的动点,将 沿 所在直线折叠,得到△ ,连接 ,则 的最小值是 .
如图,在矩形纸片 中, , ,点 是 的中点,点 是 边上的一个动点,将 沿 所在直线翻折,得到△ ,则 的长的最小值是 .

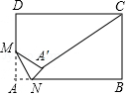
如图,在边长为3的菱形 ABCD中,∠ A=60°, M是 AD边上的一点,且 AM= AD, N是 AB边上的一动点,将△ AMN沿 MN所在直线翻折得到△ A′ MN,连接 A′ C.则 A′ C长度的最小值是 .

试题篮
()