初中数学线段的性质：两点之间线段最短试题

如图，正方形 $\mathit{ABCD}$中， $\mathit{AB}=2\sqrt{5}$， $O$是 $\mathit{BC}$边的中点，点 $E$是正方形内一动点， $\mathit{OE}=2$，连接 $\mathit{DE}$，将线段 $\mathit{DE}$绕点 $D$逆时针旋转 $90°$得 $\mathit{DF}$，连接 $\mathit{AE}$， $\mathit{CF}$．

（1）求证： $\mathit{AE}=\mathit{CF}$；

（2）若 $A$， $E$， $O$三点共线，连接 $\mathit{OF}$，求线段 $\mathit{OF}$的长．

（3）求线段 $\mathit{OF}$长的最小值．

如图，在正方形 $\mathit{ABCD}$ 中， $\mathit{AB}=2$ ， $E$ 为边 $\mathit{AB}$ 上一点， $F$ 为边 $\mathit{BC}$ 上一点．连接 $\mathit{DE}$ 和 $\mathit{AF}$ 交于点 $G$ ，连接 $\mathit{BG}$ ．若 $\mathit{AE}=\mathit{BF}$ ，则 $\mathit{BG}$ 的最小值为 　　．

一辆货车在公路（直线CD）上由点C向点D方向行驶，村庄A、B分别位于道路CD的两侧，司机师傅要在公路上选择一个货物的下货点．
（1）请在CD上确定一个下货点E，使点E到村庄A的距离最近，画出图形并写出画图的依据；
（2）请在直线CD上确定一点O，使点O到村庄A、B的距离之和最小，画出图形并写出画图的依据．

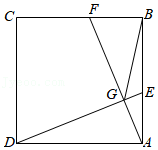
（年新疆、生产建设兵团）如图所示，某同学的家在A处，星期日他到书店去买书，想尽快赶到书店，请你帮助他选择一条最近的路线（ ）

A．A→C→D→B	B．A→C→F→B
C．A→C→E→F→B	D．A→C→M→B

如图，在中，直径垂直于不过圆心的弦，垂足为点，连接，点在上，且

（1）求证：；

（2）过点作的切线交的延长线于点，试判断与是否相等，并说明理由；

（3）设半径为4，点为中点，点在上，求线段的最小值．

对下列生活现象的解释其数学原理运用错误的是（　　）

A．把一条弯曲的道路改成直道可以缩短路程是运用了“两点之间线段最短”的原理             

B．木匠师傅在刨平的木板上任选两个点就能画出一条笔直的墨线是运用了“直线外一点与直线上各点连接的所有线段中，垂线段最短”的原理             

C．将自行车的车架设计为三角形形状是运用了“三角形的稳定性”的原理

D．将车轮设计为圆形是运用了“圆的旋转对称性”的原理

知识是用来为人类服务的，我们应该把它们用于有意义的地方．下面就两个情景请你作出评判．
情景一：从教室到图书馆，总有少数同学不走人行道而横穿草坪，这是为什么呢？试用所学数学知识来说明这个问题．

情景二：A、B是河流l两旁的两个村庄，现要在河边修一个抽水站向两村供水，问抽水站修在什么地方才能使所需的管道最短？请在图中表示出抽水站点P的位置，并说明你的理由：

你赞同以上哪种做法？你认为应用数学知识为人类服务时应注意什么？

如图，从城市A到城市B有三种不同的交通工具：汽车、火车、飞机，除去速度因素，坐飞机的时间最短是因为      ．

如图，在 $\text{Rt}\Delta \text{ABC}$中， $\angle C=90°$， $\mathit{AC}=4$， $\mathit{BC}=3$，点 $O$是 $\mathit{AB}$的三等分点，半圆 $O$与 $\mathit{AC}$相切， $M$， $N$分别是 $\mathit{BC}$与半圆弧上的动点，则 $\mathit{MN}$的最小值和最大值之和是 $($　　 $)$

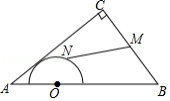
A．5B．6C．7D．8

我们知道，两点之间线段最短，因此，连接两点间线段的长度叫做两点间的距离；同理，连接直线外一点与直线上各点的所有线段中，垂线段最短，因此，直线外一点到这条直线的垂线段的长度，叫做点到直线的距离．类似地，连接曲线外一点与曲线上各点的所有线段中，最短线段的长度，叫做点到曲线的距离．依此定义，如图，在平面直角坐标系中，点 $A(2,1)$到以原点为圆心，以1为半径的圆的距离为　 　．

下列说法中，正确的有（ ）
①过两点有且只有一条直线；
②连接两点的线段叫做两点的距离；
③两点之间，垂线最短；
④若AB=BC，则点B是线段AC的中点．

A．1个

B．2个

C．3个

D．4个

下列四个生活、生产现象：
①用两个钉子就可以把木条固定在墙上；
②植树时，只要定出两棵树的位置，就能确定同一行树所在的直线；
③从A地到B地架设电线，总是尽可能沿着线段AB架设；
④把弯曲的公路改直，就能缩短路程，
其中可用公理“两点之间，线段最短”来解释的现象有（ ）

A．①②

B．①③

C．②④

D．③④

如图，平面上有四个点A、B、C、D，根据下列语句画图．

（1）画直线AB；作射线BC；画线段CD；
（2）连接AD，并将其反向延长至E，使DE=2AD；
（3）找到一点F，使点F到A、B、C、D四点距离和最短．

下列说法中正确的是（ ）

A．两点之间的所有连线中，线段最短

B．射线就是直线

C．两条射线组成的图形叫做角

D．小于平角的角可分为锐角和钝角两类

如图，从A到B有①，②，③三条路线，最短的路线是①，其理由是（ ）

A．因为它最直

B．两点确定一条直线

C．两点间的距离的概念

D．两点之间，线段最短