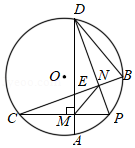
如图,在 中,点 为 的中点,弦 、 互相垂直,垂足为 , 分别与 、 相交于点 、 ,连接 、 .
(1)求证: 为 的中点.
(2)若 的半径为8, 的度数为 ,求线段 的长.
已知 , , 为直线 上一点, 为直线 上一点, ,设 , .
(1)如图,若点 在线段 上,点 在线段 上.
①如果 , ,那么 , .
②求 , 之间的关系式.
(2)是否存在不同于以上②中的 , 之间的关系式?若存在,求出这个关系式(求出一个即可);若不存在,说明理由.

定义:有一组对角互余的四边形叫做对余四边形.
理解:
(1)若四边形 是对余四边形,则 与 的度数之和为 ;
证明:
(2)如图1, 是 的直径,点 , , 在 上, , 相交于点 .
求证:四边形 是对余四边形;
探究:
(3)如图2,在对余四边形 中, , ,探究线段 , 和 之间有怎样的数量关系?写出猜想,并说明理由.

如图,在 中, ,点 , 分别在边 , 上, ,连结 , .
(1)若 ,求 , 的度数;
(2)写出 与 之间的关系,并说明理由.

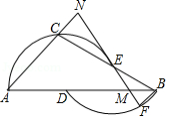
如图,已知 , 分别为 的边 , 上两点,点 , , 在 上,点 , 在 上. 为 上一点,连接 并延长交 的延长线于点 ,交 于点 .
(1)若 为 ,请将 用含 的代数式表示;
(2)若 ,请说明当 为多少度时,直线 为 的切线;
(3)在(2)的条件下,若 ,求 的值.
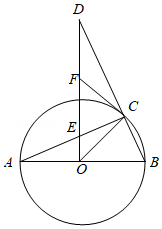
如图,是
的直径,
是
上一点,过点
作
,交
的延长线于
,交
于点
,
是
的中点,连接
.
(1)求证:是
的切线.
(2)若,求证:
.
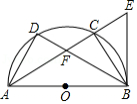
如图, 是半圆 的直径, , 是半圆 上不同于 , 的两点, , 与 相交于点 . 是半圆 所在圆的切线,与 的延长线相交于点 .
(1)求证: ;
(2)若 ,求证: 平分 .
如图, 中,点 在 边上, ,将线段 绕 点旋转到 的位置,使得 ,连接 , 与 交于点 .
(1)求证: ;
(2)若 , ,求 的度数.
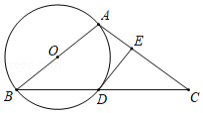
如图,在 中, ,以 为直径的 与 相交于点 ,过点 作 的切线交 于点 .
(1)求证: ;
(2)若 的半径为5, ,求 的长.
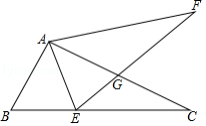
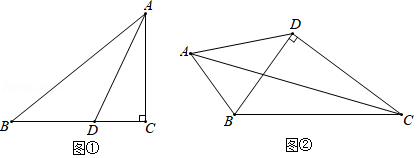
如果三角形的两个内角 与 满足 ,那么我们称这样的三角形为“准互余三角形”.
(1)若 是“准互余三角形”, , ,则 ;
(2)如图①,在 中, , , .若 是 的平分线,不难证明 是“准互余三角形”.试问在边 上是否存在点 (异于点 ,使得 也是“准互余三角形”?若存在,请求出 的长;若不存在,请说明理由.
(3)如图②,在四边形 中, , , , ,且 是“准互余三角形”,求对角线 的长.
阅读下面材料:
小明遇到这样一个问题:
如图1, 中, ,点 在 上,且 ,求证: .
小明发现,除了直接用角度计算的方法外,还可以用下面两种方法:
方法1:如图2,作 平分 ,与 相交于点 .
方法2:如图3,作 ,与 相交于点 .
(1)根据阅读材料,任选一种方法,证明 .
用学过的知识或参考小明的方法,解决下面的问题:
(2)如图4, 中,点 在 上,点 在 上,且 ,点 在 上,且 ,延长 、 ,相交于点 ,且 .
①在图中找出与 相等的角,并加以证明;
②若 ,猜想线段 与 的数量关系,并证明你的猜想.

试题篮
()