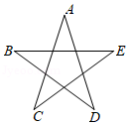
为庆祝中国共产党建党100周年,某校用红色灯带制作了一个如图所示的正五角星 , , , , 是正五角星的五个顶点),则图中 的度数是 度.
如图,在 中, ,以 为直径的半圆 交 于点 ,过点 作半圆 的切线,交 于点 .
(1)求证: ;
(2)若 , ,求 的长.

已知 , 是等腰三角形的两边长,且 , 满足 ,则此等腰三角形的周长为
| A. |
8 |
B. |
6或8 |
C. |
7 |
D. |
7或8 |
如图,在 中, ,点 , 分别在边 , 上, ,连结 , .
(1)若 ,求 , 的度数;
(2)写出 与 之间的关系,并说明理由.

如图,在 中, , ,分别以点 , 为圆心,大于 的长为半径作弧,两弧相交于 , 两点,作直线 交 于点 ,连接 ,则
.

如图, 、 、 、 是四根长度均为 的火柴棒,点 、 、 共线.若 , ,则线段 的长度是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,菱形 中, ,点 从点 出发,沿折线 方向移动,移动到点 停止.在 形状的变化过程中,依次出现的特殊三角形是
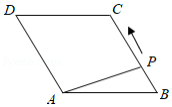
| A. |
直角三角形 等边三角形 等腰三角形 直角三角形 |
| B. |
直角三角形 等腰三角形 直角三角形 等边三角形 |
| C. |
直角三角形 等边三角形 直角三角形 等腰三角形 |
| D. |
等腰三角形 等边三角形 直角三角形 等腰三角形 |
如图,四边形 为平行四边形,连接 ,且 .请用尺规完成基本作图:作出 的角平分线与 交于点 .连接 交 于点 ,交 于点 ,猜想线段 和线段 的数量关系,并证明你的猜想.(尺规作图保留作图痕迹,不写作法)

如图,在 中, , 和 关于直线 对称,连接 ,与 相交于点 ,过点 作 ,垂足为 , 相交于点 ,若 , ,则 的值为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中, , .分别以点 , 为圆心,大于 的长为半径画弧,两弧交于 , 两点,直线 交 于点 ,连接 .以点 为圆心, 为半径画弧,交 延长线于点 ,连接 .若 ,则 的周长为 .

试题篮
()