(本题12分)已知两个全等的直角三角形纸片ABC、DEF,如图(1)放置,点B、D重合,点F在BC上,AB与EF交于点G,∠C=∠EFB=90°,∠E=∠ABC=30°,AB=DE=4.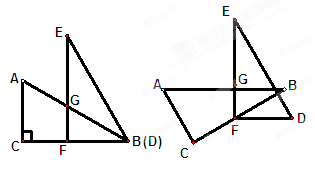
(1)求证:△EGB是等腰三角形
(2)若纸片DEF不动,问△ABC绕点F逆时针旋转最小 度时,四边形ACDE成为以ED为底的梯形(如图(2)),求此梯形的高。
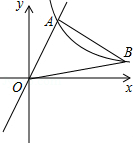
如图,在平面直角坐标系中,经过点 的双曲线 同时经过点 ,且点 在点 的左侧,点 的横坐标为 , ,则 的值为 .
中, , , ,过点 的直线把 分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是 .
有一张等腰三角形纸片, , ,小明将它沿虚线 剪开,得到 和四边形 两张纸片(如图所示),且满足 ,则下列五个数据 ,3, ,2, 中可以作为线段 长的有 个.

如图,在菱形 中, , ,点 是这个菱形内部或边上的一点.若以 , , 为顶点的三角形是等腰三角形,则 , , 两点不重合)两点间的最短距离为 .

试题篮
()