我们规定:三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差.如图1,在 中, 是 边上的中线, 与 的“极化值”就等于 的值,可记为 △ .
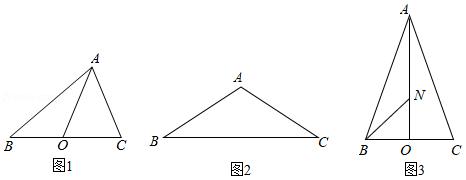
(1)在图1中,若 , , , 是 边上的中线,则 △ , △ ;
(2)如图2,在 中, , ,求 △ 、 △ 的值;
(3)如图3,在 中, , 是 边上的中线,点 在 上,且 .已知 △ , △ ,求 的面积.
思维启迪:
(1)如图1, , 两点分别位于一个池塘的两端,小亮想用绳子测量 , 间的距离,但绳子不够长,聪明的小亮想出一个办法:先在地上取一个可以直接到达 点的点 ,连接 ,取 的中点 (点 可以直接到达 点),利用工具过点 作 交 的延长线于点 ,此时测得 米,那么 , 间的距离是 200 米.
思维探索:
(2)在 和 中, , ,且 , ,将 绕点 顺时针方向旋转,把点 在 边上时 的位置作为起始位置(此时点 和点 位于 的两侧),设旋转角为 ,连接 ,点 是线段 的中点,连接 , .
①如图2,当 在起始位置时,猜想: 与 的数量关系和位置关系分别是 ;
②如图3,当 时,点 落在 边上,请判断 与 的数量关系和位置关系,并证明你的结论;
③当 时,若 , ,请直接写出 的值.

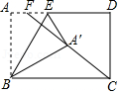
如图,矩形 中, , ,点 为 上一点,且 ,将 沿 翻折,得到△ ,连接 并延长,与 相交于点 ,则 的长为 .
现有 、 两个大型储油罐,它们相距 ,计划修建一条笔直的输油管道,使得 、 两个储油罐到输油管道所在直线的距离都为 ,输油管道所在直线符合上述要求的设计方案有 种.
如图, ,以点 为圆心,以任意长为半径作弧交 , 于 , 两点;分别以 , 为圆心,以大于 的长为半径作弧,两弧相交于点 ;以 为端点作射线 ,在射线 上截取线段 ,则 点到 的距离为

A.6B.2C.3D.
如图所示,直线 和圆 相切于点 ,交直径 的延长线于点 .过点 作 的垂线,交 于点 ,交圆 于点 .作平行四边形 ,连接 , , .
(1)求证: ;
(2)求 及 的大小.

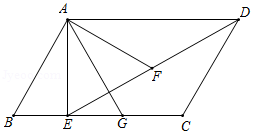
如图,在平行四边形 中, 是 边上的高,点 是 的中点, 与 关于 对称, 与 关于 对称.
(1)求证: 是等边三角形;
(2)若 ,求 的面积.
如图,已知 , 是 平分线上一点, ,交 于点 , ,垂足为点 ,且 ,则 等于

A.1B.2C.4D.8
如图,在 中, , 是 上一点, ,点 是射线 上的一个动点, ,则当 为直角三角形时, 的长为 .

四边形具有不稳定性.如图,矩形 按箭头方向变形成平行四边形 ,当变形后图形面积是原图形面积的一半时,则 .

已知等边 的边长为12, 是 上的动点,过 作 于点 ,过 作 于点 ,过 作 于点 .当 与 重合时, 的长是
A.3B.4C.8D.9
试题篮
()