小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.
(1)温故:如图1,在中,
于点
,正方形
的边
在
上,顶点
,
分别在
,
上,若
,
,求正方形
的边长(用
,
表示).
(2)操作:如何画出这个正方形呢?
如图2,小波画出了图1的,然后按数学家波利亚在《怎样解题》中的方法进行操作:先在
上任取一点
,画正方形
,使点
,
在
边上,点
在
内,然后连结
,并延长交
于点
,画
于点
,
交
于点
,
于点
,得到四边形
.
(3)推理:证明图2中的四边形是正方形.
(4)拓展:小波把图2中的线段称为“波利亚线”,在该线上截取
,连结
,
(如图
,当
时,求“波利亚线”
的长(用
,
表示).
请帮助小波解决“温故”、“推理”、“拓展”中的问题.

如图,在矩形 中, 是边 上一点, , ,垂足为 .将四边形 绕点 顺时针旋转 ,得到四边形 , 所在的直线分别交直线 于点 ,交直线 于点 ,交 于点 . 所在的直线分别交直线 于点 ,交直线 于点 ,连接 交 于点 .
(1)如图1,求证:四边形 是正方形;
(2)如图2,当点 和点 重合时.
①求证: ;
②若 , ,求线段 的长;
(3)如图3,若 交 于点 , ,求 的值.

已知抛物线过点
,
两点,与
轴交于点
,
.
(1)求抛物线的解析式及顶点的坐标;
(2)过点作
,垂足为
,求证:四边形
为正方形;
(3)点为抛物线在直线
下方图形上的一动点,当
面积最大时,求点
的坐标;
(4)若点为线段
上的一动点,问:
是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.

如图,在 中, , ,点 为 的中点,连接 ,将线段 绕点 顺时针旋转 得到线段 ,且 交线段 于点 , 的平分线 交 于点 .
(1)如图1,若 ,则线段 与 的数量关系是 , ;
(2)如图2,在(1)的条件下,过点 作 交 于点 ,连接 , .
①试判断四边形 的形状,并说明理由;
②求证: ;
(3)如图3,若 , ,过点 作 交 于点 ,连接 , ,请直接写出 的值(用含 的式子表示).
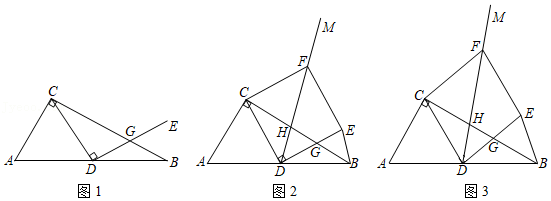
如图,在 中,对角线 , , , 为 的中点, 为边 上一点,直线 交 于点 ,连结 , .下列结论不成立的是
A.四边形 为平行四边形
B.若 ,则四边形 为矩形
C.若 ,则四边形 为菱形
D.若 ,则四边形 为正方形
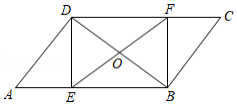
如图,点 、 、 、 分别是四边形 边 、 、 、 的中点.则下列说法:
①若 ,则四边形 为矩形;
②若 ,则四边形 为菱形;
③若四边形 是平行四边形,则 与 互相平分;
④若四边形 是正方形,则 与 互相垂直且相等.
其中正确的个数是
A.1B.2C.3D.4
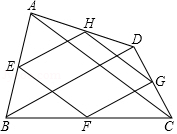
如图,在直角坐标系中, 的直角边 在 轴上, , ,反比例函数 的图象经过 边的中点 .
(1)求这个反比例函数的表达式;
(2)若 与 成中心对称,且 的边 在 轴的正半轴上,点 在这个函数的图象上.
①求 的长;
②连接 , ,证明四边形 是正方形.

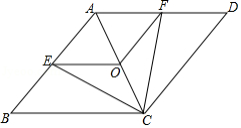
已知:如图,在菱形 中,点 , , 分别为 , , 的中点,连接 , , , .
(1)求证: ;
(2)当 与 满足什么关系时,四边形 是正方形?请说明理由.
设 , , , 是反比例函数 图象上的任意四点,现有以下结论:
①四边形 可以是平行四边形;
②四边形 可以是菱形;
③四边形 不可能是矩形;
④四边形 不可能是正方形.
其中正确的是 .(写出所有正确结论的序号)
如图,在 和 中, , , .延长 至点 ,使 ;延长 至点 ,使 .连接 , , , .延长 交 于点 .
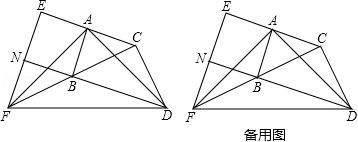
(1)求证: ;
(2)求证: ;
(3)试判断四边形 的形状,并说明理由.
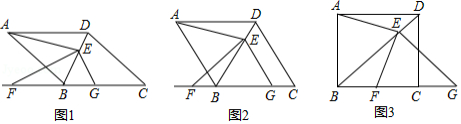
在菱形 中,点 为对角线 上一点,点 , 在直线 上,且 , .
(1)如图1,求证: ;
(2)如图2,当 时,求证: ;
(3)如图3,当 ,点 在线段 上时,线段 , , 的数量关系如何?(请直接写出你猜想的结论)
下列说法正确的是
A.一组对边平行另一组对边相等的四边形是平行四边形
B.对角线互相垂直平分的四边形是菱形
C.对角线相等的四边形是矩形
D.对角线互相垂直且相等的四边形是正方形
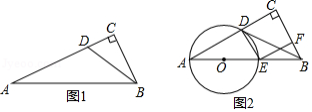
如图1, 中, ,点 在 上, ,过 、 两点的圆的圆心 在 上.
(1)利用直尺和圆规在图1中画出 (不写作法,保留作图痕迹,并用黑色水笔把线条描清楚);
(2)判断 所在直线与(1)中所作的 的位置关系,并证明你的结论;
(3)设 交 于点 ,连接 ,过点 作 , 为垂足,若点 是线段 的黄金分割点(即 ,如图2,试说明四边形 是正方形).
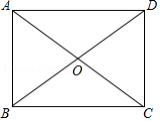
如图所示,已知平行四边形 ,对角线 , 相交于点 , .
(1)求证:平行四边形 是矩形;
(2)请添加一个条件使矩形 为正方形.
试题篮
()