初中数学垂径定理试题

如图，在半径为3的 $\odot O$ 中， $\mathit{AB}$ 是直径， $\mathit{AC}$ 是弦， $D$ 是 $\stackrel{̂}{\mathit{AC}}$ 的中点， $\mathit{AC}$ 与 $\mathit{BD}$ 交于点 $E$ ．若 $E$ 是 $\mathit{BD}$ 的中点，则 $\mathit{AC}$ 的长是 $($ 　　 $)$

A．

$\frac{5}{2}\sqrt{3}$

B．

$3\sqrt{3}$

C．

$3\sqrt{2}$

D．

$4\sqrt{2}$

如图，点 $A$ ， $B$ ， $C$ ， $D$ 在 $\odot O$ 上， $\mathit{OA}\perp \mathit{BC}$ ，垂足为 $E$ ．若 $\angle \mathit{ADC}=30°$ ， $\mathit{AE}=1$ ，则 $\mathit{BC}=($ 　　 $)$

A．

2

B．

4

C．

$\sqrt{3}$

D．

$2\sqrt{3}$

如图， $\odot O$ 中， $\mathit{OC}\perp \mathit{AB}$ ， $\angle \mathit{APC}=28°$ ，则 $\angle \mathit{BOC}$ 的度数为 $($ 　　 $)$

A．

$14°$

B．

$28°$

C．

$42°$

D．

$56°$

如图， $\odot O$ 的直径 $\mathit{CD}=20$ ， $\mathit{AB}$ 是 $\odot O$ 的弦， $\mathit{AB}\perp \mathit{CD}$ ，垂足为 $M$ ， $\mathit{OM}:\mathit{OC}=3:5$ ，则 $\mathit{AB}$ 的长为 $($ 　　 $)$

A．

8

B．

12

C．

16

D．

$2\sqrt{91}$

在半径为的中，弦垂直于弦，垂足为，，则　     　．

如图，是的直径，点在直径上与，不重合），，且，连接，与交于点，在上取一点，使．

（1）求证：是的切线；

（2）若是的中点，，求的长．

如图，已知 $\stackrel{̂}{\mathit{AB}}$ 的半径为5，所对的弦 $\mathit{AB}$ 长为8，点 $P$ 是 $\stackrel{̂}{\mathit{AB}}$ 的中点，将 $\stackrel{̂}{\mathit{AB}}$ 绕点 $A$ 逆时针旋转 $90°$ 后得到 $\stackrel{̂}{\mathit{AB}\text{'}}$ ，则在该旋转过程中，点 $P$ 的运动路径长是 $($ 　　 $)$

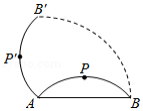
A．

$\frac{\sqrt{5}}{2}\pi$

B．

$\sqrt{5}\pi$

C．

$2\sqrt{5}\pi$

D．

$2\pi$

如图， $\mathit{AD}$ 是 $\odot O$ 的直径， $\mathit{BC}$ 是弦，四边形 $\mathit{OBCD}$ 是平行四边形， $\mathit{AC}$ 与 $\mathit{OB}$ 相交于点 $P$ ，下列结论错误的是 $($ 　　 $)$

A．

$\mathit{AP}=2\mathit{OP}$

B．

$\mathit{CD}=2\mathit{OP}$

C．

$\mathit{OB}\perp \mathit{AC}$

D．

$\mathit{AC}$ 平分 $\mathit{OB}$

如图，是的直径，点为上一点，点是半径上一动点（不与，重合），过点作射线，分别交弦，于，两点，在射线上取点，使．

（1）求证：是的切线；

（2）当点是的中点时，

①若，判断以，，，为顶点的四边形是什么特殊四边形，并说明理由；

②若，且，求的长．

如图，为的直径，为上一点，过点的切线交的延长线于点，为弦的中点，，，若点为直径上的一个动点，连接，当是直角三角形时，的长为　　．

如图，在中，是直径，是弦，，连接交于点，．

（1）求证：是的切线．

（2）过点作于，交于，已知，，求的长．

如图， $\mathit{PA}$ 、 $\mathit{PB}$ 为圆 $O$ 的切线，切点分别为 $A$ 、 $B$ ， $\mathit{PO}$ 交 $\mathit{AB}$ 于点 $C$ ， $\mathit{PO}$ 的延长线交圆 $O$ 于点 $D$ ，下列结论不一定成立的是 $($ 　　 $)$

A．

$\mathit{PA}=\mathit{PB}$

B．

$\angle \mathit{BPD}=\angle \mathit{APD}$

C．

$\mathit{AB}\perp \mathit{PD}$

D．

$\mathit{AB}$ 平分 $\mathit{PD}$

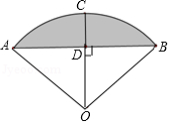
《九章算术》是我国古代数学成就的杰出代表作，其中《方田》章计算弧田面积所用的经验公式是：弧田面积（弦矢矢．弧田是由圆弧和其所对的弦围成（如图中的阴影部分），公式中“弦”指圆弧所对弦长，“矢”等于半径长与圆心到弦的距离之差，运用垂径定理（当半径弦时，平分可以求解．现已知弦米，半径等于5米的弧田，按照上述公式计算出弧田的面积为　　平方米．

如图，在中，，的平分线交于点，点在上，以为直径的经过点．

（1）求证：①是的切线；

②；

（2）若点是劣弧的中点，且，试求阴影部分的面积．

如图， $\odot P$ 与 $x$ 轴交于点 $A(-5,0)$ ， $B(1,0)$ ，与 $y$ 轴的正半轴交于点 $C$ ．若 $\angle \mathit{ACB}=60°$ ，则点 $C$ 的纵坐标为 $($ 　　 $)$

A．

$\sqrt{13}+\sqrt{3}$

B．

$2\sqrt{2}+\sqrt{3}$

C．

$4\sqrt{2}$

D．

$2\sqrt{2}+2$