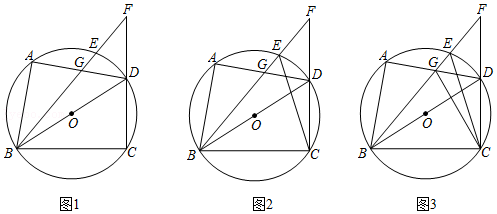
如图1,四边形 ABCD 内接于 ⊙O , BD 为直径, ̂AD 上存在点 E ,满足 ^AE=^CD ,连结 BE 并延长交 CD 的延长线于点 F , BE 与 AD 交于点 G .
(1)若 ∠DBC=α ,请用含 α 的代数式表示 ∠AGB .
(2)如图2,连结 CE , CE=BG .求证: EF=DG .
(3)如图3,在(2)的条件下,连结 CG , AD=2 .
①若 tan∠ADB=√32 ,求 ΔFGD 的周长.
②求 CG 的最小值.
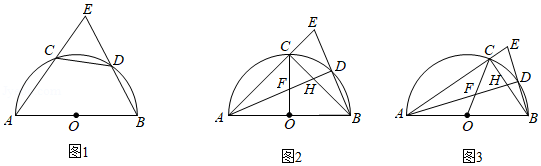
如图1, O 为半圆的圆心, C 、 D 为半圆上的两点,且 ̂BD=̂CD .连接 AC 并延长,与 BD 的延长线相交于点 E .
(1)求证: CD=ED ;
(2) AD 与 OC , BC 分别交于点 F , H .
①若 CF=CH ,如图2,求证: CF⋅AF=FO⋅AH ;
②若圆的半径为2, BD=1 ,如图3,求 AC 的值.
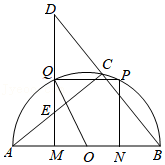
如图,点 O 为以 AB 为直径的半圆的圆心,点 M , N 在直径 AB 上,点 P , Q 在 ̂AB 上,四边形 MNPQ 为正方形,点 C 在 ̂QP 上运动(点 C 与点 P , Q 不重合),连接 BC 并延长交 MQ 的延长线于点 D ,连接 AC 交 MQ 于点 E ,连接 OQ .
(1)求 sin∠AOQ 的值;
(2)求 AMMN 的值;
(3)令 ME=x , QD=y ,直径 AB=2R(R>0 , R 是常数),求 y 关于 x 的函数解析式,并指明自变量 x 的取值范围.
试题篮
()