如图,在 中, 为直径, .点 为弦 的中点,点 为 上任意一点.则 的大小可能是
A. B. C. D.
如图, 是 的直径,弦 ,垂足为点 ,连接 , .如果 , ,那么图中阴影部分的面积是

A. B. C. D.
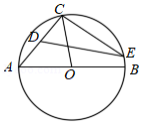
如图,在四边形 中,以 为直径的半圆 经过点 , . 与 相交于点 , ,分别延长 , 相交于点 , , .则 的长是 .
如图,在 中, ,以 为直径的 与 相交于点 ,过点 作 的切线交 于点 .
(1)求证: ;
(2)若 的半径为5, ,求 的长.
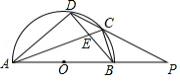
如图,点 在以 为直径的 上,点 是半圆 的中点,连接 , , , .过点 作 交 的延长线于点 .
(1)求证:直线 是 的切线;
(2)若 , ,求 , 的长.
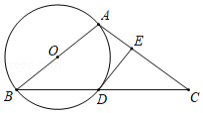
如图, , 为 上两点,且在直径 两侧,连结 交 于点 , 是 上一点, .
(1)求证: .
(2)点 关于 的对称点为 ,连结 .当点 落在直径 上时, , ,求 的半径.
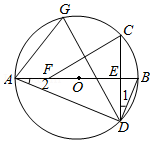
如图,在 中, ,将 沿直线 翻折得到 ,连接 交 于点 . 是线段 上的点,连接 . 是 的外接圆与 的另一个交点,连接 , .
(1)求证: 是直角三角形;
(2)求证: ;
(3)当 , 时,在线段 上存在点 ,使得 和 互相平分,求 的值.

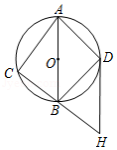
如图, 内接于 , 为 的直径, , ,连结 ,弦 分别交 , 于点 , ,其中点 是 的中点.
(1)求证: .
(2)求 的长.

定义:三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角.
(1)如图1, 是 中 的遥望角,若 ,请用含 的代数式表示 .
(2)如图2,四边形 内接于 , ,四边形 的外角平分线 交 于点 ,连结 并延长交 的延长线于点 .求证: 是 中 的遥望角.
(3)如图3,在(2)的条件下,连结 , ,若 是 的直径.
①求 的度数;
②若 , ,求 的面积.

如图, 是等边 的内切圆,分别切 , , 于点 , , , 是 上一点,则 的度数是
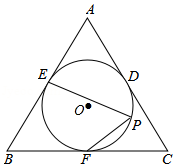
A. B. C. D.
试题篮
()