如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连接AD1、BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分面积为S,则下列结论:

①△A1AD1≌△CC1B;
②当x=1时,四边形ABC1D1是菱形;
③当x=2时,△BDD1为等边三角形;
④S= (x-2)2(0≤x≤2).
(x-2)2(0≤x≤2).
其中正确的是 (将所有正确答案的序号都填写在横线上)
已知关于 的一元二次方程
的一元二次方程 的两个实数根
的两个实数根 、
、 的值分别是□ABCD的两边AB、AD的长.
的值分别是□ABCD的两边AB、AD的长.
(1)如果 ,试求□ABCD的周长;
,试求□ABCD的周长;
(2)当 为何值时,□ABCD是菱形?
为何值时,□ABCD是菱形?
如图,在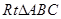 中,
中,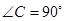 ,
,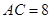 ,
,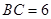 ,点
,点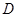 是
是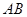 上的一个动点(不与
上的一个动点(不与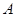 、
、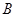 两点重合),
两点重合),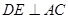 于点
于点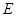 ,
,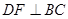 于点
于点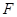 ,点
,点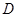 从靠近点
从靠近点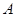 的某一点向点
的某一点向点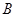 移动,矩形
移动,矩形 的周长变化情况是( )
的周长变化情况是( )
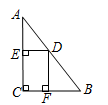
| A.逐渐减小 | B.逐渐增大 | C.先增大后减小 | D.先减小后增大 |
如图,E是矩形ABCD的边CD上的一点,BE交AC于点O,已知△OCE和△OBC的面积分别为2和8.
(1)求△OAB和四边形AOED的面积;
(2)若BE⊥AC,求BE的长.
下列命题中,不正确的是( ).
| A.一个四边形如果既是矩形又是菱形,那么它一定是正方形 |
| B.有一个角是直角,且有一组邻边相等的平行四边形是正方形 |
| C.有一组邻边相等的矩形是正方形 |
| D.两条对角线垂直且相等的四边形是正方形 |
△ABC中,D、E、F分别是BC、CA、AB边的中点,那么四边形AFDE的周长等于( ).

(A)AB+AC (B)AD+BC (C) (D)BC+AC
(D)BC+AC
有一个边长为11cm的正方形和一个长为15cm,宽为5cm的矩形,要作一个面积为这两个图形面积之和的正方形,则此正方形边长应为__________cm.
试题篮
()