如图,点 是 的边 上一点,以 为半径的 与边 相切于点 ,与边 , 分别相交于点 , ,且 .
(1)求证: ;
(2)当 , 时,求 的长.
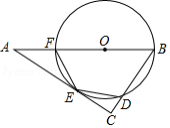
如图, 是 的直径, 为弦, 的平分线交 于点 ,过点 的切线交 的延长线于点 .
求证:(1) ;
(2) .

如图,已知 的半径为 ,射线 经过点 , ,射线 与 相切于点 . 、 两点同时从点 出发,点 以 的速度沿射线 方向运动,点 以 的速度沿射线 方向运动,设运动时间为 .
(1)求 的长;
(2)当直线 与 相切时,求证: ;
(3)当 为何值时,直线 与 相切?

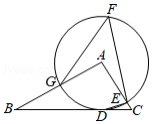
如图,在 中, ,以点 为圆心,3为半径的圆与边 相切于点 ,与 , 分别交于点 和点 ,点 是优弧 上一点, ,则 的度数是
| A. |
|
B. |
|
C. |
|
D. |
|
如图, 是 的直径,点 为线段 上一点(不与 , 重合),作 ,交 于点 ,作直径 ,过点 的切线交 的延长线于点 ,作 于点 ,连接 .
(1)求证: 平分 ;
(2)求证: ;
(3)当 且 时,求劣弧 的长度.

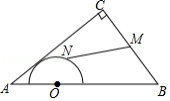
如图,在 中, , , ,点 是 的三等分点,半圆 与 相切, , 分别是 与半圆弧上的动点,则 的最小值和最大值之和是
A.5B.6C.7D.8
如图, 为 的切线,切点为 ,连接 、 , 与 交于点 ,延长 与 交于点 ,连接 .若 ,则 的度数为

A. B. C. D.
如图, 为 的直径, 、 是 的切线,切点分别为点 、 ,点 为线段 上的一个动点,连接 , , ,已知 , ,当 的值最小时,则 的值为

A. B. C. D.
如图,AB是半圆O的直径,点P是BA延长线上一点,PC是⊙O的切线,切点为C,过点B作BD⊥PC交PC的延长线于点D,连接BC.求证:
(1)∠PBC=∠CBD;
(2)BC2=AB•BD.
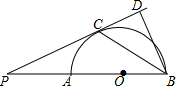
如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是 上不与点A、点C重合的一个动点,连接AD、CD,若∠APB=80°,则∠ADC的度数是( )
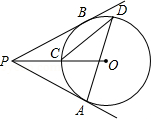
A.15°B.20°C.25°D.30°
如图,在Rt△ABC中, ,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.
(1)求证:AD平分∠CAB;
(2)若 于点H,FH平分 .
①试判断DF与DH的数量关系,并说明理由;
②求⊙O的半径.

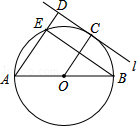
如图, AB为⊙ O的直径,直线 l与⊙ O相切于点 C, ,垂足为 D, AD交⊙ O于点 E,连接 OC、 BE.若 , ,则线段 DC的长为 .
试题篮
()