已知:如图, ,射线 上一点 .
求作:等腰 ,使线段 为等腰 的底边,点 在 内部,且点 到 两边的距离相等.
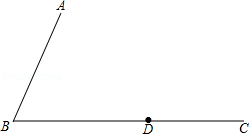
在一次数学活动课中,某数学小组探究求环形花坛(如图所示)面积的方法,现有以下工具;①卷尺;②直棒 ;③ 型尺 所在的直线垂直平分线段 .
(1)在图1中,请你画出用 形尺找大圆圆心的示意图(保留画图痕迹,不写画法);
(2)如图2,小华说:“我只用一根直棒和一个卷尺就可以求出环形花坛的面积,具体做法如下:
将直棒放置到与小圆相切,用卷尺量出此时直棒与大圆两交点 , 之间的距离,就可求出环形花坛的面积.”如果测得 ,请你求出这个环形花坛的面积.

点 、 为半径是3的圆周上两点,点 为 的中点,以线段 、 为邻边作菱形 ,顶点 恰在该圆直径的三等分点上,则该菱形的边长为
A. 或 B. 或 C. 或 D. 或
已知 和点 ,如图.
(1)以点 为一个顶点作△ ,使△ ,且△ 的面积等于 面积的4倍;(要求:尺规作图,不写作法,保留作图痕迹)
(2)设 、 、 分别是 三边 、 、 的中点, 、 、 分别是你所作的△ 三边 、 、 的中点,求证: △ .
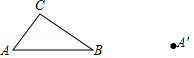
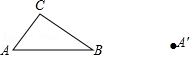
已知 和点 ,如图.
(1)以点 为一个顶点作△ ,使△ ,且△ 的面积等于 面积的4倍;(要求:尺规作图,不写作法,保留作图痕迹)
(2)设 、 、 分别是 三边 、 、 的中点, 、 、 分别是你所作的△ 三边 、 、 的中点,求证: △ .
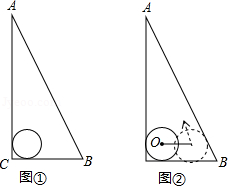
如图, 是一块直角三角板,且 , ,现将圆心为点 的圆形纸片放置在三角板内部.
(1)如图①,当圆形纸片与两直角边 、 都相切时,试用直尺与圆规作出射线 ;(不写作法与证明,保留作图痕迹)
(2)如图②,将圆形纸片沿着三角板的内部边缘滚动1周,回到起点位置时停止,若 ,圆形纸片的半径为2,求圆心 运动的路径长.
如图,已知等边 ,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹)
(1)作 的外心 ;
(2)设 是 边上一点,在图中作出一个正六边形 ,使点 ,点 分别在边 和 上.
如图,已知 ,及线段 , .
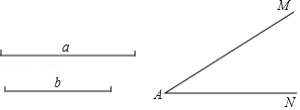
(1)仅用没有刻度的直尺和圆规分别在射线 、 上确定点 、点 ,使得 , (保留作图痕迹,不要作法);
(2)若 , , ,则 的面积为 .
如图,已知 ,及线段 , .

(1)仅用没有刻度的直尺和圆规分别在射线 、 上确定点 、点 ,使得 , (保留作图痕迹,不要作法);
(2)若 , , ,则 的面积为 .
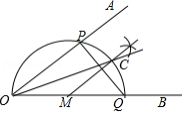
已知 ,作图.
步骤1:在 上任取一点 ,以点 为圆心, 长为半径画半圆,分别交 、 于点 、 ;
步骤2:过点 作 的垂线交 于点 ;
步骤3:画射线 .
则下列判断:① ;② ;③ ;④ 平分 ,其中正确的个数为
A.1B.2C.3D.4
“直角”在初中几何学习中无处不在.
如图,已知 ,请仿照小丽的方式,再用两种不同的方法判断 是否为直角(仅限用直尺和圆规).

如图,已知 中,
(1)尺规作图:按下列要求完成作图(保留作图痕迹,请标明字母)
①作线段 的垂直平分线 ,交 于点 ;
②连接 并延长,在 的延长线上截取 ,使得 ;
③连接 、
(2)判断四边形 的形状,并说明理由.

如图, ,以点 为圆心,1为半径画 与 的延长线交于点 ,过点 画 的垂线,垂线与 的一个交点为 ,连接
(1)线段 的长等于 ;
(2)请在图中按下列要求逐一操作,并回答问题:
①以点 为圆心,以线段 的长为半径画弧,与射线 交于点 ,使线段 的长等于
②连 ,在 上画出点 ,使 的长等于 ,请写出画法,并说明理由.

试题篮
()