初中数学推理与论证选择题

某届世界杯的小组比赛规则：四个球队进行单循环比赛（每两队赛一场），胜一场得3分，平一场得1分，负一场得0分，某小组比赛结束后，甲、乙、丙、丁四队分别获得第一、二、三、四名，各队的总得分恰好是四个连续奇数，则与乙打平的球队是 $($　　 $)$

A．甲B．甲与丁C．丙D．丙与丁

一个大矩形按如图方式分割成九个小矩形，且只有标号为①和②的两个小矩形为正方形，在满足条件的所有分割中．若知道九个小矩形中 $n$个小矩形的周长，就一定能算出这个大矩形的面积，则 $n$的最小值是 $($　　 $)$

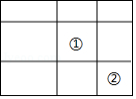
A．3B．4C．5D．6

甲、乙、丙、丁4人进行乒乓球单循环比赛（每两个人都要比赛一场），结果甲胜了丁，并且甲、乙、丙胜的场数相同，则丁胜的场数是 $($　　 $)$

A．3B．2C．1D．0

一个整数的所有正约数之和可以按如下方法求得，如：

$6=2\times 3$，则6的所有正约数之和 $(1+3)+(2+6)=(1+2)\times (1+3)=12$；

$12=2^2\times 3$，则12的所有正约数之和 $(1+3)+(2+6)+(4+12)=(1+2+2^2)\times (1+3)=28$；

$36=2^2\times 3^2$，则36的所有正约数之和

$(1+3+9)+(2+6+18)+(4+12+36)=(1+2+2^2)\times (1+3+3^2)=91$．

参照上述方法，那么200的所有正约数之和为 $($　　 $)$

A．420B．434C．450D．465

张奶奶从邮递员手中接过所订的报纸，不经意间从这份报纸中抽出一张，发现第8版和第21版在同一张纸上．请你判断一下，这份报纸共有（  ）

A．27版

B．28版

C．29版

D．以上答案都不对