如图,已知一次函数 的图象与反比例函数 的图象交于点A(﹣1,2)和点B,点C在y轴上.
(1)当△ABC的周长最小时,求点C的坐标;
(2)当 x+b<
x+b< 时,请直接写出x的取值范围.
时,请直接写出x的取值范围.

如图,在矩形中,
,
,点
是边
的中点,反比例函数
的图象经过点
,交
边于点
,直线
的解析式为
.
(1)求反比例函数的解析式和直线
的解析式;
(2)在轴上找一点
,使
的周长最小,求出此时点
的坐标;
(3)在(2)的条件下,的周长最小值是 .

如图,在四边形中,
,
,点
为
的中点,点
为
的中点,
,连接
、
、
.
(1)判断四边形的形状,并说明理由;
(2)如果,
,点
为
上的动点,求
的周长的最小值.
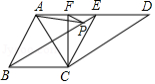
如图,在菱形中,连结
、
交于点
,过点
作
于点
,以点
为圆心,
为半径的半圆交
于点
.
①求证:是
的切线.
②若且
,求图中阴影部分的面积.
③在②的条件下,是线段
上的一动点,当
为何值时,
的值最小,并求出最小值.

在平面直角坐标系中, 为原点,点 ,点 ,把 绕点 逆时针旋转,得△ ,点 , 旋转后的对应点为 , ,记旋转角为 .
(Ⅰ)如图①,若 ,求 的长;
(Ⅱ)如图②,若 ,求点 的坐标;
(Ⅲ)在(Ⅱ)的条件下,边 上 的一点 旋转后的对应点为 ,当 取得最小值时,求点 的坐标(直接写出结果即可)

如图,已知抛物线与
轴交于
、
两点.与
轴交于
点.且
,
.
(1)求抛物线的函数表达式;
(2)在抛物线的对称轴上是否存在一点
,使
周长最小?若存在,求出点
的坐标;若不存在,请说明理由.
(3)连接、
,在抛物线
上是否存在一点
,使
?若存在,求出点
的坐标;若不存在,请说明理由.

(年新疆、生产建设兵团)如图,直线 与x轴、y轴分别交于点A、B.抛物线
与x轴、y轴分别交于点A、B.抛物线 经过A、B,并与x轴交于另一点C,其顶点为P,
经过A、B,并与x轴交于另一点C,其顶点为P,
(1)求a,k的值;
(2)在图中求一点Q,A.B、C为顶点的四边形是平行四边形,请直接写出相应的点Q的坐标;
(3)抛物线的对称轴上是否存在一点M,使△ABM的周长最小?若存在,求△ABM的周长;若不存在,请说明理由;
(4)抛物线的对称轴是上是否存在一点N,使△ABN是以AB为斜边的直角三角形?若存在,求出N点的坐标,若不存在,请说明理由.
试题篮
()