七巧板是我国祖先的一项卓越创造.下列四幅图中有三幅是小明用如图所示的七巧板拼成的,则不是小明拼成的那副图是

A.
B.
C.
D.
如图,13个边长为1的小正方形,排列形式如图,把它们分割,使分割后能拼成一个大正方形.请在如图所示的网格中(网格的边长为 中,用直尺作出这个大正方形.
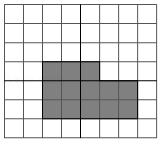
观察下列各方格图中阴影部分所示的图形(每一小方格的边长为 ,如果将它们沿方格边线或对角线剪开重新拼接,不能拼成正方形的是
A. B.
B.
C. D.
D.
如图1,分别沿长方形纸片 和正方形纸片 的对角线 , 剪开,拼成如图2所示的 ,若中间空白部分四边形 恰好是正方形,且 的面积为50,则正方形 的面积为

| A. |
24 |
B. |
25 |
C. |
26 |
D. |
27 |
问题提出:如何将边长为 ,且 为整数)的正方形分割为一些 或 的矩形( 的矩形指边长分别为 , 的矩形)?
问题探究:我们先从简单的问题开始研究解决,再把复杂问题转化为已解决的问题.
探究一:
如图①,当 时,可将正方形分割为五个 的矩形.
如图②,当 时,可将正方形分割为六个 的矩形.
如图③,当 时,可将正方形分割为五个 的矩形和四个 的矩形
如图④,当 时,可将正方形分割为八个 的矩形和四个 的矩形
如图⑤,当 时,可将正方形分割为九个 的矩形和六个 的矩形

探究二:
当 ,11,12,13,14时,分别将正方形按下列方式分割:

所以,当 ,11,12,13,14时,均可将正方形分割为一个 的正方形、一个 的正方形和两个 的矩形.显然, 的正方形和 的矩形均可分割为 的矩形,而 的正方形是边长分别为5,6,7,8,9的正方形,用探究一的方法可分割为一些 或 的矩形.
探究三:
当 ,16,17,18,19时,分别将正方形按下列方式分割:

请按照上面的方法,分别画出边长为18,19的正方形分割示意图.
所以,当 ,16,17,18,19时,均可将正方形分割为一个 的正方形、一个 的正方形和两个 的矩形.显然, 的正方形和 的矩形均可分割为 的矩形,而 的正方形又是边长分别为5,6,7,8,9的正方形,用探究一的方法可分割为一些 或 的矩形.
问题解决:如何将边长为 ,且 为整数)的正方形分割为一些 或 的矩形?请按照上面的方法画出分割示意图,并加以说明.
实际应用:如何将边长为61的正方形分割为一些 或 的矩形?(只需按照探究三的方法画出分割示意图即可)
如图,矩形纸片 中, , .将该矩形纸片剪去3个等腰直角三角形,所有剪法中剩余部分面积的最小值是

A.6B.3C.2.5D.2
(1)阅读材料:
教材中的问题,如图1,把5个边长为1的小正方形组成的十字形纸板剪开,使剪成的若干块能够拼成一个大正方形,小明的思考:因为剪拼前后的图形面积相等,且5个小正方形的总面积为5,所以拼成的大正方形边长为 ,故沿虚线 剪开可拼成大正方形的一边,请在图1中用虚线补全剪拼示意图.
(2)类比解决:
如图2,已知边长为2的正三角形纸板 ,沿中位线 剪掉 ,请把纸板剩下的部分 剪开,使剪成的若干块能够拼成一个新的正三角形.
①拼成的正三角形边长为 ;
②在图2中用虚线画出一种剪拼示意图.
(3)灵活运用:
如图3,把一边长为 的正方形彩纸剪开,用剪成的若干块拼成一个轴对称的风筝,其中 ,延长 、 分别与 、 交于点 、 ,点 、 分别为 、 的中点,在线段 和 处用轻质钢丝做成十字形风筝龙骨,在图3的正方形中画出一种剪拼示意图,并求出相应轻质钢丝的总长度.(说明:题中的拼接都是不重叠无缝隙无剩余)

如图,在等腰三角形纸片 中, , ,沿底边 上的高 剪成两个三角形,用这两个三角形拼成平行四边形,则这个平行四边形较长的对角线的长是 .

请用割补法作图,将一个锐角三角形经过一次或两次分割后,重新拼成一个与原三角形面积相等的平行四边形(只要求用一种方法画出图形,把相等的线段作相同的标记).

如图是用8块 型瓷砖(白色四边形)和8块 型瓷砖(黑色三角形)不重叠、无空隙拼接而成的一个正方形图案,图案中 型瓷砖的总面积与 型瓷砖的总面积之比为

| A. |
|
B. |
|
C. |
|
D. |
|
在数学拓展课上,小明发现:若一条直线经过平行四边形对角线的交点,则这条直线平分该平行四边形的面积.如图是由5个边长为1的小正方形拼成的图形, 是其中4个小正方形的公共顶点,小强在小明的启发下,将该图形沿着过点 的某条直线剪一刀,把它剪成了面积相等的两部分,则剪痕的长度是

| A. |
|
B. |
|
C. |
|
D. |
|
试题篮
()