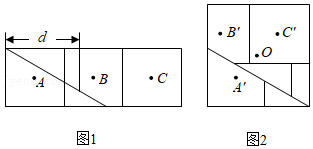
图1是邻边长为2和6的矩形,它由三个小正方形组成,将其剪拼成不重叠、无缝隙的大正方形(如图 ,则图1中所标注的 的值为 ;记图1中小正方形的中心为点 , , ,图2中的对应点为点 , , .以大正方形的中心 为圆心作圆,则当点 , , 在圆内或圆上时,圆的最小面积为 .
将一张圆形纸片(圆心为点 沿直径 对折后,按图1分成六等份折叠得到图2,将图2沿虚线 剪开,再将 展开得到如图3的一个六角星.若 ,则 的度数为 .

综合实践活动课上,小亮将一张面积为 ,其中一边 为 的锐角三角形纸片(如图 ,经过两刀裁剪,拼成了一个无缝隙、无重叠的矩形 (如图 ,则矩形的周长为 .

如图所示的图案由三个叶片组成,绕点 旋转 后可以和自身重合.若每个叶片的面积为 , 为 ,则图中阴影部分的面积之和为 .

中国古代数学家刘徽在《九章算术注》中,给出了证明三角形面积公式的出入相补法.如图所示,在 中,分别取 、 的中点 、 ,连接 ,过点 作 ,垂足为 ,将 分割后拼接成矩形 .若 , ,则 的面积是 .

在综合实践课上,老师要求同学用正方形纸片剪出正三角形且正三角形的顶点都在正方形边上.小红利用两张边长为2的正方形纸片,按要求剪出了一个面积最大的正三角形和一个面积最小的正三角形.则这两个正三角形的边长分别是 .
用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案,每块大正方形地砖面积为 ,小正方形地砖面积为 ,依次连接四块大正方形地砖的中心得到正方形 .则正方形 的面积为 .(用含 , 的代数式表示)

如图,等边三角形纸片 的边长为6, , 是边 上的三等分点.分别过点 , 沿着平行于 , 方向各剪一刀,则剪下的 的周长是 .

将两条邻边长分别为 ,1的矩形纸片剪成四个等腰三角形纸片(无余纸片),各种剪法剪出的等腰三角形中,其中一个等腰三角形的腰长可以是下列数中的 (填序号).
① ,②1,③ ,④ ,⑤ .
如图,在 纸板中, , , , 是 上一点,过点 沿直线剪下一个与 相似的小三角形纸板,如果有4种不同的剪法,那么 长的取值范围是 .

如图,在等腰三角形纸片 中, , ,沿底边 上的高 剪成两个三角形,用这两个三角形拼成平行四边形,则这个平行四边形较长的对角线的长是 .

试题篮
()