如图,将 沿 边向右平移得到 , 交 于点 .若 . .则 的值为
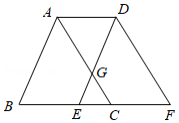
| A. |
2 |
B. |
4 |
C. |
6 |
D. |
8 |
如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形.下列图形中,平移重合图形是
A.平行四边形B.等腰梯形C.正六边形D.圆
小军同学在网格纸上将某些图形进行平移操作,他发现平移前后的两个图形所组成的图形可以是轴对称图形.如图所示,现在他将正方形 从当前位置开始进行一次平移操作,平移后的正方形顶点也在格点上,则使平移前后的两个正方形组成轴对称图形的平移方向有

A.3个B.4个C.5个D.无数个
如图,将 沿 边上的中线 平移到△ 的位置,已知 的面积为9,阴影部分三角形的面积为4.若 ,则 等于

A.2B.3C. D.
在平面直角坐标系 中,将一块含有 角的直角三角板如图放置,直角顶点 的坐标为 ,顶点 的坐标为 ,顶点 恰好落在第一象限的双曲线上,现将直角三角板沿 轴正方向平移,当顶点 恰好落在该双曲线上时停止运动,则此时点 的对应点 的坐标为

A. , B. C. , D.
如图,在正方形网格(每个小正方形的边长都是 中,若将 沿 的方向平移 长,得 、 的对应点分别为 、 ,则 长为

A.1B.2C. D.3
如图,菱形 的对角线 , 交于点 , , ,将 沿点 到点 的方向平移,得到△ .当点 与点 重合时,点 与点 之间的距离为

A.6B.8C.10D.12
如图,把 沿着 的方向平移到 的位置,它们重叠部分的面积是 面积的一半,若 ,则 移动的距离是

A. B. C. D.
如图,在菱形 中, ,它的一个顶点 在反比例函数 的图象上,若将菱形向下平移2个单位,点 恰好落在函数图象上,则反比例函数解析式为

A. B. C. D.
对于平面图形上的任意两点 , ,如果经过某种变换得到新图形上的对应点 , ,保持 ,我们把这种变换称为“等距变换”,下列变换中不一定是等距变换的是
A.平移B.旋转C.轴对称D.位似
在 中, , ,点 、 ,点 在第一象限内,双曲线 经过点 .将 沿 轴向上平移 个单位长度,使点 恰好落在双曲线上,则 的值为

A.2B. C.3D.
试题篮
()