(本题12分)已知两个全等的直角三角形纸片ABC、DEF,如图(1)放置,点B、D重合,点F在BC上,AB与EF交于点G,∠C=∠EFB=90°,∠E=∠ABC=30°,AB=DE=4.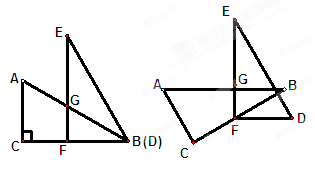
(1)求证:△EGB是等腰三角形
(2)若纸片DEF不动,问△ABC绕点F逆时针旋转最小 度时,四边形ACDE成为以ED为底的梯形(如图(2)),求此梯形的高。
如图,将含30°角的直角三角尺ABC绕点B顺时针旋转 
150°后得到△EBD,连结CD.若AB="4cm." 则△BCD的面积
为( )
A.4 B.2 C.3 D.2
如图,在 中, , , ,将 绕点 逆时针旋转角 得到△ ,并使点 落在 边上,则点 所经过的路径长为 .(结果保留

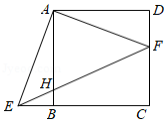
如图, 是线段 上除端点外的一点,将 绕正方形 的顶点 顺时针旋转 ,得到 .连接 交 于点 .下列结论正确的是
| A. |
|
B. |
|
| C. |
|
D. |
|
如图,长为4cm,宽为3cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为A→A1→A2,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°,则点A翻滚到A2位置时共走过的路径长为( )

| A.10cm | B. cm cm |
C. cm cm |
D. cm cm |
如图,在4×4的正方形网格中,每个小正方形的边长为1,若将△AOC绕点O顺时针旋转90°得到△BOD,则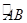 的长为( )
的长为( )

| A.π | B.6π | C.3π | D.1.5π |
如图,将△ ABC绕点 A逆时针旋转55°得到△ ADE,若 且 于点 F,则∠ BAC的度数为( )

| A. |
65° |
B. |
70° |
C. |
75° |
D. |
80° |
如图,在 中, , .将 绕点 逆时针方向旋转 ,得到△ ,连接 .则线段 的长为

| A. |
1 |
B. |
|
C. |
|
D. |
|
如图,四边形ABCD是正方形,△ADE绕着点A旋转90°后到达△ABF的位置,连接EF,则△AEF的形状是( )

| A.等腰三角形 | B.锐角三角形 | C.等腰直角三角形 | D.等边三角形 |
如图,在 中, ,将 绕点 逆时针旋转得到 ,点 , 的对应点分别为 , ,连接 .当点 , , 在同一条直线上时,下列结论一定正确的是

| A. |
|
B. |
|
C. |
|
D. |
|
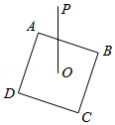
定义:平面上一点到图形最短距离为 ,如图, ,正方形 边长为2, 为正方形中心,当正方形 绕 旋转时,则 的取值范围为 .
如图, 的顶点 , ,点 在 轴的正半轴上,延长 交 轴于点 .将 绕点 顺时针旋转得到△ ,当点 的对应点 落在 上时, 的延长线恰好经过点 ,则点 的坐标为

| A. |
, |
B. |
, |
C. |
, |
D. |
, |
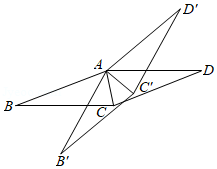
如图.将菱形 绕点 逆时针旋转 得到菱形 , .当 平分 时, 与 满足的数量关系是
| A. |
|
B. |
|
C. |
|
D. |
|
试题篮
()