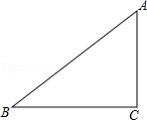
如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.

如图,在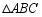 中,
中,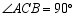 ,
,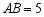 ,
,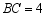 ,将
,将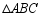 绕点
绕点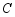 顺时针旋转
顺时针旋转 ,若点
,若点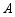 ,
,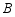 的对应点分别是点
的对应点分别是点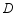 ,
, ,画出旋转后的三角形,并求点
,画出旋转后的三角形,并求点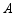 与点
与点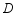 之间的距离.(不要求尺规作图)
之间的距离.(不要求尺规作图)
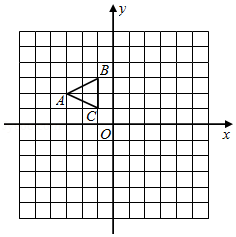
如图, 在平面直角坐标系中,顶点的坐标分别为 , , .
(1)画出与 关于 轴对称的△ ;
(2)将 绕点 顺时针旋转 得到△ , 弧是点 所经过的路径,则旋转中心 的坐标为 ;
(3)求图中阴影部分的面积(结果保留 .

如图所示的平面直角坐标系中, 的三个顶点坐标分别为 , , ,请按如下要求画图:
(1)以坐标原点 为旋转中心,将 顺时针旋转 ,得到△ ,请画出△ ;
(2)以坐标原点 为位似中心,在 轴下方,画出 的位似图形△ ,使它与 的位似比为 .
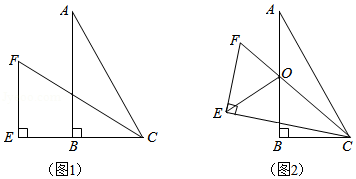
如图1,点在线段
上,
,
,
,
.
(1)点到直线
的距离是 ;
(2)固定,将
绕点
按顺时针方向旋转
,使得
与
重合,并停止旋转.
①请你在图1中用直尺和圆规画出线段经旋转运动所形成的平面图形(用阴影表示,保留画图痕迹,不要求写画法).该图形的面积为 ;
②如图2,在旋转过程中,线段与
交于点
,当
时,求
的长.
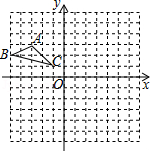
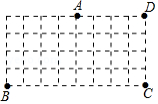
在 的网格中建立如图的平面直角坐标系,四边形 的顶点坐标分别为 , , , .仅用无刻度的直尺在给定网格中按下列步骤完成画图,并回答问题:
(1)将线段 绕点 逆时针旋转 ,画出对应线段 ;
(2)在线段 上画点 ,使 (保留画图过程的痕迹);
(3)连接 ,画点 关于直线 的对称点 ,并简要说明画法.

如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,的三个顶点
、
、
均在格点上.
(1)将向左平移5个单位得到△
,并写出点
的坐标;
(2)画出△绕点
顺时针旋转
后得到的△
,并写出点
的坐标;
(3)在(2)的条件下,求△在旋转过程中扫过的面积(结果保留
.

在边长为1的正方形网格中如图所示.
①以点为位似中心,作出
的位似图形△
,使其位似比为
.且△
位于点
的异侧,并表示出
的坐标.
②作出绕点
顺时针旋转
后的图形△
.
③在②的条件下求出点经过的路径长.
如图,在边长为1个单位长度的小正方形组成的网格中,的三个顶点均在格点上,将
绕点
按顺时针方向旋转
,点
的对应点为点
,连接
,则线段
.

如图,在每个小正方形的边长为1的网格中,的顶点
,
,
均在格点上,
的大小为 (度
;
(Ⅱ)在如图所示的网格中,是
边上任意一点,以
为中心,取旋转角等于
,把点
逆时针旋转,点
的对应点为
,当
最短时,请用无刻度的直尺,画出点
,并简要说明点
的位置是如何找到的(不要求证明) .

如图是由边长为1的小正方形组成的网格,每个小正方形的顶点叫做格点,点
,
,
,
均在格点上,在网格中将点
按下列步骤移动:
第一步:点绕点
顺时针旋转
得到点
;
第二步:点绕点
顺时针旋转
得到点
;
第三步:点绕点
顺时针旋转
回到点
.
(1)请用圆规画出点经过的路径;
(2)所画图形是 对称图形;
(3)求所画图形的周长(结果保留.
如图,圆心角都是900的扇形OAB与扇形OCD叠放在一起,OA=3, OC=1,分别连接AC、BD,则图中阴影部分的面积为( )

A. B.
B. C.
C. D.
D.
试题篮
()