如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
(1)求证: =AB·AD;
=AB·AD;
(2)若AD=4,AB=6,求 的值.
的值.
在平面直角坐标系中,已知点A(﹣4,2),B(﹣6,﹣4),以原点O为位似中心,相似比为 ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )
| A.(﹣2,1) |
| B.(﹣8,4 |
| C.(﹣8,4)或(8,﹣4) |
| D.(﹣2,1)或(2,﹣1) |
如图,在△ABC中,DE∥BC,分别交AB,AC于点D、E.若AD=3,DB=2,BC=6,则DE的长为 .

已知△ABC中,AB=10,AC=8,D、E分别是AB、AC上的点,且AD=4,以A、D、E为顶点的三角形和△ABC相似,则AE的长是( )
A.5 B. C.
C. D.5或
D.5或
下列各组数中的四条线段能成比例线段的是( )
| A.a=6,b=4,c=10,d=5 |
| B.a=3,b=7,c=2,d=9 |
| C.a=2,b=4,c=3,d=6 |
| D.a=4,b=11,c=3,d=2 |
如图,以点O为位似中心,将△ABC放大得到△DEF.若AD=OA,则△ABC与△DEF的面积之比为( )

| A.1:2 | B.1:4 | C.1:5 | D.1:6 |
如图,以点O为支点的杠杆,在A端用竖直向上的拉力将重为G的物体匀速拉起,当杠杆OA水平时,拉力为F;当杠杆被拉至OA1时,拉力为F1,过点B1作B1C⊥OA,过点A1作A1D⊥OA,垂足分别为点C、D.①△OB1C∽△OA1D; ②OA•OC=OB•OD;③OC•G=OD•F1;④F=F1.
其中正确的说法有( )

A.1个 B.2个 C.3个 D.4个
小明、小亮利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为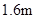 的小明
的小明 的影子
的影子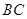 长是
长是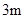 ,而小亮
,而小亮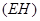 刚好在路灯灯泡的正下方
刚好在路灯灯泡的正下方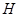 点,并测得
点,并测得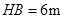 .
.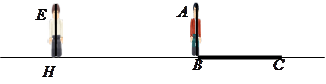
(1)请在图中画出形成影子的光线,交确定路灯灯泡所在的位置 ;
;
(2)求路灯灯泡的垂直高度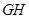 .
.
如图,P为线段AB上一点,AD与BC交于E,∠CPD=∠A=∠B,BC交PD于F,AD交PC
于G,则图中相似三角形有( )

| A.1对 | B.2对 | C.3对 | D.4对 |
试题篮
()