如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的边长为( )

| A.9 | B.12 | C.15 | D.18 |
(本小题满分10分)如图,在平面直角坐标系中,点A、B、C、P的坐标分别为(0,1)、(-1,0)、(1,0)、(-1,-1)。
(1)求经过A、B、C三点的抛物线的表达式;
(2)以P为位似中心,将△ABC放大,使得放大后的△A1B1C1
与△OAB对应线段的比为3:1,请在右图网格中画出放大
后的△A1B1C1;(所画△A1B1C1与△ABC在点P同侧);(3)经过A1、B1、C1三点的抛物线能否由(1)中的抛物线平
移得到?请说明理由。
如图,在□ABCD中,点E为AD的中点,连接BE交AC于点F,则AF∶CF= ( )
| A.1∶2 | B.1∶3 | C.2∶3 | D.2∶5 |
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
如图,矩形 的四个顶点分别在菱形 的四条边上, .将 , 分别沿边 , 折叠,当重叠部分为菱形且面积是菱形 面积的 时,则 为
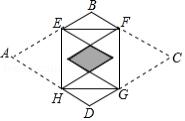
A. B.2C. D.4
如图,在正方形网格中,每个小正方形的边长均相等.网格中三个多边形(分别标记为①,②,③ 的顶点均在格点上.被一个多边形覆盖的网格线中,竖直部分线段长度之和记为 ,水平部分线段长度之和记为 ,则这三个多边形中满足 的是
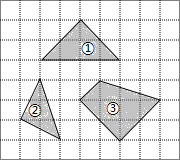
| A. |
只有② |
B. |
只有③ |
C. |
②③ |
D. |
①②③ |
如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(4,0),B(0,3).点C的坐标为(0,m),过点C作CE⊥AB于点E,点D为x轴正半轴的一动点,且满足OD=2OC,连结DE,以DE,DA为边作▱DEFA.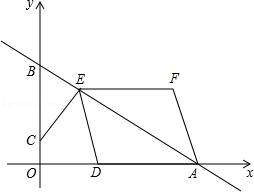
(1)当m=1时,求AE的长.
(2)当0<m<3时,若▱DEFA为矩形,求m的值;
(3)是否存在m的值,使得▱DEFA为菱形?若存在,直接写出m的值;若不存在,请说明理由.
如图,在△ABC中,D、E分别是AB、AC的中点,则△ADE与△ABC的面积比为 .

如图,在△ABC中,AD是角平分钱,点E在AC上,且∠EAD=∠ADE.
(1)求证:△DCE∽△BCA;
(2)若AB=3,AC=4.求DE的长.
在比例尺是1:8000的某市地图上,若一条路的长度约25cm,则它的实际长度约为______;对于地图上3cm×5cm的矩形广场相应的实际占地面积为_____平方千米.
如图,在矩形ABCD中,AB=3,AD=4,将此矩形折叠,使点D落在AB边上的点E处,折痕为FH,点C落在点Q处,EQ与BC交于点G,设AE=x,四边形EFHQ的面积为y,则y关于x的函数解析式是 .
如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上)
(1)若△CEF与△ABC相似.
①当AC=BC=2时,AD的长为 ;
②当AC=3,BC=4时,AD的长为 ;
(2)当点D是AB的中点时,△CEF与△ABC相似吗?请说明理由.
试题篮
()