已知点C是线段AB的黄金分割点,且CB>AC,则下列等式中成立的是 ( )
A.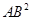 =AC·CB =AC·CB |
B.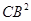 =AC·AB =AC·AB |
C. =CB·AB =CB·AB |
D. =2BC·AB =2BC·AB |
如图,将△ABC的高AD三等分,过每个分点作底边的平行线,把△ABC的面积分成三部分S1,S2,S3,则S1:S2:S3=( )
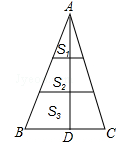
| A.1:2:3 | B.1:4:9 | C.1:3:5 | D.1:9:25 |
如图,线段AB两个端点的坐标分别是A(6,4),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的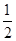 后得到线段CD,则端点C的坐标为( )
后得到线段CD,则端点C的坐标为( )
| A.(3,2) | B.(4,1) | C.(3,1) | D.(4,2) |
如图,P是Rt△ABC斜边AB上任意一点(A、B两点除外),过点P作一直线,使截得的三角形与Rt△ABC相似,这样的直线可以作( )

A、1条 B、2条 C、3条 D、4条
若△ABC∽△A′B′C′,∠A=40°,∠B=60°,则∠C′等于( )
| A.40° | B.60° | C.80° | D.100° |
如图,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点O,若 ,
, ,
,
则 的值为( )
的值为( )

A. |
B. |
C. |
D. |
如图,小明作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积.然后分别取△A1B1C1三边的中点A2、B2、C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积.用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积…,由此可得,第10个正△A10B10C10的面积是( )

A. |
B. |
C. |
D. |
将三角形纸片△ABC按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=6,BC=8,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是( )

A. |
B. |
C. 或4 或4 |
D. 或4 或4 |
如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是( )

| A.AB2=BC•BD | B.AB2=AC•BD | C.AB AB•AD=BD•BC | D.AB•AD=AD•CD |
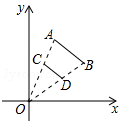
如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的 后得到线段CD,则端点C的坐标为( )
后得到线段CD,则端点C的坐标为( )

| A.(3,3) | B.(4,3) | C.(3,1) | D.(4,1) |
如图,M是Rt△ABC的斜边BC上异于B、C的一定点,过M点作直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有( )

A.1条 B.2条 C.3条 D.4条
试题篮
()