初中数学相似多边形的性质选择题

已知线段AB，点P是它的黄金分割点，AP＞BP，设以AP为边的等边三角形的面积为S₁，以PB、AB为直角边的直角三角形的面积为S₂，则S₁与S₂的关系是                 （     ）
A．S₁＞S₂        B．S₁＜S₂           C．S₁=S₂         D．S₁≥S₂

△ABC与△A′B′C′是位似图形，且△ABC与△A′B′C′的位似比是1：2，已知△ABC的面积是3，则△A′B′C′的面积是（     ）

A．3

B．6

C．9

D．12

如图，为测量某树的高度，小明用长为2m的竹竿作测量工具，移动竹竿，使竹竿顶端、树的顶端的影子恰好落在地面的同一点O，此时竹竿与这一点相距6m，与树相距15m，则树的高度为（     ）

A．4m

B．5m

C．7m

D．9m

若，则的值是（  ）

A．

B．

C．

D．

如图，△ABC中，DE∥BC，DE=1，AD=2，DB=3，则BC的长是（  ）

A．

B．

C．

D．

如图，点A，B，C，D的坐标分别是（1，7），（1，1），（4，1），（6，1），以C，D，E为顶点的三角形与△ABC相似，则点E的坐标不可能是（  ）

A．（6，0）

B．（6，3）

C．（6，5）

D．（4，2）

如图，在△ABC中，∠C=90°，AC＝BC＝4，D是AB的中点，点E、F分别在AC、BC边上运动（点E不与点A、C重合），且保持AE=CF，连接DE、DF、EF．在运动变化过程中，下列结论：①△DFE是等腰直角三角形；②四边形CEDF不可能为正方形；③四边形CEDF的面积随点E位置的改变而发生变化；④点C、E、D、F四点在同一个圆上，且该圆面积最小为4π；⑤DE•DF+CE•CF的值是定值为8，其中正确结论的个数是（ ）

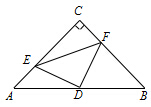
A．4                B．3                 C．2                   D．1

如图，△ABC中，AB=AC=2，∠BAC=20°，动点P、Q分别在直线BC上运动，且始终保持∠PAQ=100°．设BP=x，CQ=y，则y与x之间的函数关系用图象大致可表示为（ ）

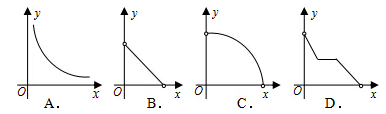
如图，等边△ABC的边长为2，DE是它的中位线，则下列三个结论：①DE＝1；②△CDE∽△CAB；③△CDE与△CAB的面积之比为1：4．其中正确的有 （ ）

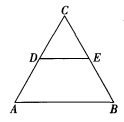
A．0个

B．1个

C．2个

D．3个

若△ABC∽△A'B'C'，∠A＝40°，∠C＝110°，则∠B'的度数为 （ ）

A．30°

B．50°

C．40°

D．70°

如图，在△ABC中，D、E分别是AB、BC上的点，且DE∥AC，若，则的值（ ）

A．1∶5        B．1∶9         C．1∶12        D．1∶16

下列条件不能判定△ABC与△DEF相似的是（     ）

A．

B．，

C．∠A=∠D，∠B=∠E

D．，∠B=∠E

如图，阳光从教室的窗户射入室内，窗户框AB在地面上的影长DE＝1．8 m，窗户下沿到地面的距离BC＝1 m，EC＝1．2 m，那么窗户的高AB为  （  ）                        

A．2．16m

B．1．86m

C．1．6m

D．1．5m

如图，已知直线a∥b∥c，直线m、n与直线a、b、c分别交于点A、C、E、B、D、F，AC=4，CE=6，BD=3，则BF等于 （  ）                                            

A．7     B．8    C．7．5    D．8．5

如图，线段AB两个端点的坐标分别为A（6，6），B（8，2），以原点O为位似中心，在第一象限内将线段AB缩小为原来的后得到线段CD，则端点C的坐标为 （  ） 

A．（3，3）

B．（4，3）

C．（3，1）

D．（4，1）