初中数学相似多边形的性质解答题

数学兴趣小组想测量一棵树的高度，在阳光下，一名同学测得一根长为1m的竹竿的影长为0.8m，同时另一名同学测量一棵树的高度时，发现树的影子不全落在地面上，有一部分影子落在教学楼的墙壁上，其中，落在墙壁上的影长为1.5m，落在地面上的影长为4.8m，求树的高为多少米?

（本题满分12分 第（1）小题6分，第（2）小题6分）
已知：如图，在△ABC中，BD⊥AC于点D， CE⊥AB于点E，EC和BD相交于点O，联接DE．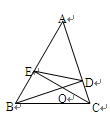

（1）求证：△EOD∽△BOC；
（2）若S_△EOD＝16，S_△BOC＝36，求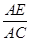的值．

如图, ΔABC是等边三角形,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F。

(1)求证：ΔABD≌ΔBCE.
(2)ΔAEF与ΔABE相似吗?请说明理由.
(3)成立吗?请说明理由.

(7分)如图，点E为矩形ABCD中CD边上的一点，沿BE折叠为，点F落在AD上。

（1）求证：∽
（2）若，求的值

如图，是等边三角形，CE是外角平分线，点D在AC上，连结BD并延长与CE交于点E.

（1）直接写出的度数等于__________°；
（2）求证：△ABD∽△CED；
（3）若AB=12，AD=2CD，求BE的长.

如图，中，AB=AC=，，BD平分.

（1）图中有      个等腰三角形；
（2）求BC的长（用含的代数式表示）.

如图，△ABC是等边三角形，CE是外角平分线，点D在AC上，连结BD并延长与CE交于点E．

(1)求证：△ABD∽△CED；
(2)若AB＝6，AD＝2CD，求BE的长．

在中，cm ，cm ，动点以1cm/s 的速度从点出发到点止，动点以2cm/s 的速度从点出发到点止，且两点同时运动，当以点、、为顶点的三角形与相似时，求运动的时间.

如图，在中，，，点、分别在边、上，且，设， . 求与的函数关系式；

如图，在中，是边上一点，连结，，，，求的长．

如图，在平行四边形ABCD中，的平分线分别与、交于点、．

（1）求证：；
（2）当时，求的值．

如图△ABC中，AB=AC，∠A=120°

（1）用直尺和圆规作AB的垂直平分线，分别交BC，AB于点M，N（保留痕迹，不写作法）
（2）猜想CM与BM有何数量关系，并证明你的猜想。

已知如图AD为△ABC上的高，E为AC上一点BE交AD于F且有BF=AC，FD=CD
求证：BE⊥AC

如图，△ABC中，AB=AC，点E是AC上一点，ED⊥BC于点D，DE的延长线交BA的延长线于点F。

求证：△AEF是等腰三角形

（本题10分）
如图，在正△ABC中，点D是AC的中点，点E在BC上，且 ＝ ．求证：

（1）△ABE∽△DCE；
（2），求