初中数学相似三角形的应用选择题

一个三角形木架三边长分别是 $75\mathit{cm}$ ， $100\mathit{cm}$ ， $120\mathit{cm}$ ，现要再做一个与其相似的三角形木架，而只有长为 $60\mathit{cm}$ 和 $120\mathit{cm}$ 的两根木条．要求以其中一根为一边，从另一根截下两段作为另两边（允许有余料），则不同的截法有 $($ 　　 $)$

A．

一种

B．

两种

C．

三种

D．

四种

如图，在 $\mathit{\Delta ABC}$ 中， $\mathit{BC}=120$ ，高 $\mathit{AD}=60$ ，正方形 $\mathit{EFGH}$ 一边在 $\mathit{BC}$ 上，点 $E$ ， $F$ 分别在 $\mathit{AB}$ ， $\mathit{AC}$ 上， $\mathit{AD}$ 交 $\mathit{EF}$ 于点 $N$ ，则 $\mathit{AN}$ 的长为 $($ 　　 $)$

A．

15

B．

20

C．

25

D．

30

如图所示，某校数学兴趣小组利用标杆 $\mathit{BE}$ 测量建筑物的高度，已知标杆 $\mathit{BE}$ 高 $1.5m$ ，测得 $\mathit{AB}=1.2m$ ， $\mathit{BC}=12.8m$ ，则建筑物 $\mathit{CD}$ 的高是 $($ 　　 $)$

A．

$17.5m$

B．

$17m$

C．

$16.5m$

D．

$18m$

如图，在横格作业纸（横线等距）上画一条直线，与横格线交于 $A$ ， $B$ ， $C$ 三点，则 $\mathit{BC}:\mathit{AC}$ 等于 $($ 　　 $)$

A．

$2:3$

B．

$2:5$

C．

$3:4$

D．

$3:5$

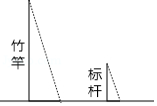
《孙子算经》是中国古代重要的数学著作， 成书于约一千五百年前， 其中有首歌谣： 今有竿不知其长， 量得影长一丈五尺， 立一标杆， 长一尺五寸， 影长五寸， 问竿长几何？意即： 有一根竹竿不知道有多长， 量出它在太阳下的影子长一丈五尺， 同时立一根一尺五寸的小标杆， 它的影长五寸 （提 示： 1 丈 $=10$ 尺， 1 尺 $=10$ 寸） ，则竹竿的长为 $($ 　　 $)$

A．	A ． 五丈B ． 四丈五尺C ． 一丈D ． 五尺

（年新疆、生产建设兵团）如图，李明打网球时，球恰好打过网，且落在离网4m的位置上，则网球的击球的高度h为          ．

（年贵州省黔南州）如图是小明设计用手电来测量都匀南沙州古城墙高度的示意图，点P处放一水平的平面镜，光线从点A出发经过平面镜反射后刚好射到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，且测得AB=1．2米，BP=1．8米，PD=12米，那么该古城墙的高度是      米（平面镜的厚度忽略不计）．