初中数学相似三角形的应用选择题

图1是装了液体的高脚杯示意图（数据如图），用去一部分液体后如图2所示，此时液面 $\mathit{AB}=($ 　　 $)$

A．

$1\mathit{cm}$

B．

$2\mathit{cm}$

C．

$3\mathit{cm}$

D．

$4\mathit{cm}$

如图，已知“人字梯”的5个踩档把梯子等分成6份，从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF，tanα=，则“人字梯”的顶端离地面的高度AD是（    ）

A．144cm

B．180cm

C．240cm

D．360cm

如图，在钝角三角形ABC中，AB＝6cm，AC＝12cm，动点D从A点出发到B点止，动点E从C点出发到A点止．点D运动的速度为1cm/秒，点E运动的速度为2cm/秒．如果两点同时运动，那么当以点A、D、E为顶点的三角形与△ABC相似时，运动的时间是（  ）

A.3秒或4.8秒
B.3秒
C.4.5秒
D.4.5秒或4.8秒

如图．利用标杆 $\mathit{BE}$测量建筑物的高度．已知标杆 $\mathit{BE}$高 $1.2m$，测得 $\mathit{AB}=1.6m$． $\mathit{BC}=12.4m$．则建筑物 $\mathit{CD}$的高是 $($　　 $)$

A． $9.3m$B． $10.5m$C． $12.4m$D． $14m$

如图，在一斜边长 $30\mathit{cm}$的直角三角形木板（即 $\text{Rt}\Delta \text{ACB})$中截取一个正方形 $\mathit{CDEF}$，点 $D$在边 $\mathit{BC}$上，点 $E$在斜边 $\mathit{AB}$上，点 $F$在边 $\mathit{AC}$上，若 $\mathit{AF}:\mathit{AC}=1:3$，则这块木板截取正方形 $\mathit{CDEF}$后，剩余部分的面积为 $($　　 $)$

A． $200c{m}^2$B． $170c{m}^2$C． $150c{m}^2$D． $100c{m}^2$

学校门口的栏杆如图所示，栏杆从水平位置 $\mathit{BD}$绕 $O$点旋转到 $\mathit{AC}$位置，已知 $\mathit{AB}\perp \mathit{BD}$， $\mathit{CD}\perp \mathit{BD}$，垂足分别为 $B$， $D$， $\mathit{AO}=4m$， $\mathit{AB}=1.6m$， $\mathit{CO}=1m$，则栏杆 $C$端应下降的垂直距离 $\mathit{CD}$为 $($　　 $)$

A． $0.2m$B． $0.3m$C． $0.4m$D． $0.5m$

圆桌面（桌面中间有一个直径为0.4m的圆洞）正上方的灯泡（看作一个点）发出的光线照射平行于地面的桌面后，在地面上形成如图所示的圆环形阴影．已知桌面直径为1.2m，桌面离地面1m，若灯泡离地面3m，则地面圆环形阴影的面积是（　　）

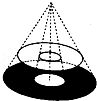
A．0.324πm²B．0.288πm²C．1.08πm²D．0.72πm²

为测量操场上旗杆的高度，小丽同学想到了物理学中平面镜成像的原理．她拿出随身携带的镜子和卷尺，先将镜子放在脚下的地面上，然后后退，直到她站直身子刚好能从镜子里看到旗杆的顶端 $E$，标记好脚掌中心位置为 $B$，测得脚掌中心位置 $B$到镜面中心 $C$的距离是 $50\mathit{cm}$，镜面中心 $C$距离旗杆底部 $D$的距离为 $4m$，如图所示．已知小丽同学的身高是 $1.54m$，眼睛位置 $A$距离小丽头顶的距离是 $4\mathit{cm}$，则旗杆 $\mathit{DE}$的高度等于 $($　　 $)$

A． $10m$B． $12m$C． $12.4m$D． $12.32m$

如图，小明为了测量一凉亭的高度AB（顶端A到水平地面BD的距离），在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE（DE＝BC＝0.5米，A、B、C三点共线），把一面镜子水平放置在平台上的点G处，测得CG＝15米，然后沿直线CG后退到点E处，这时恰好在镜子里看到凉亭的顶端A，测得EG＝3米，小明身高1.6米，则凉亭的高度AB约为（　　）

A．8.5米B．9米C．9.5米D．10米

志远要在报纸上刊登广告，一块10 cm×5 cm的长方形版面要付广告费180元，他要把该版面的边长都扩大为原来的3倍，在每平方厘米版面广告费相同的情况下，他该付广告费（　　）

A．

540元

B．

1080元

C．

1620元

D．

1800元

“今有井径五尺，不知其深，立五尺木于井上，从木末望水岸，入径四寸，问井深几何？”这是我国古代数学《九章算术》中的“井深几何”问题，它的题意可以由图获得，则井深为 $($　　 $)$

A．1.25尺B．57.5尺C．6.25尺D．56.5尺

有3个正方形如图所示放置，阴影部分的面积依次记为S₁，S₂，则S₁：S₂等于（　　）

A．1：B．1：2C．2：3D．4：9

如图，树 $\mathit{AB}$ 在路灯 $O$ 的照射下形成投影 $\mathit{AC}$ ，已知路灯高 $\mathit{PO}=5m$ ，树影 $\mathit{AC}=3m$ ，树 $\mathit{AB}$ 与路灯 $O$ 的水平距离 $\mathit{AP}=4.5m$ ，则树的高度 $\mathit{AB}$ 长是 $($ 　　 $)$

A．

$2m$

B．

$3m$

C．

$\frac{3}{2}m$

D．

$\frac{10}{3}m$

一个三角形木架三边长分别是 $75\mathit{cm}$ ， $100\mathit{cm}$ ， $120\mathit{cm}$ ，现要再做一个与其相似的三角形木架，而只有长为 $60\mathit{cm}$ 和 $120\mathit{cm}$ 的两根木条．要求以其中一根为一边，从另一根截下两段作为另两边（允许有余料），则不同的截法有 $($ 　　 $)$

A．

一种

B．

两种

C．

三种

D．

四种

如图，三角板在灯光照射下形成投影，三角板与其投影的相似比为 $2:5$，且三角板的一边长为 $8\mathit{cm}$．则投影三角板的对应边长为 $($　　 $)$

A． $20\mathit{cm}$B． $10\mathit{cm}$C． $8\mathit{cm}$D． $3.2\mathit{cm}$