如图,已知等边三角形 与反比例函数 的图象交于 、 两点,将 沿直线 翻折,得到 ,点 的对应点为点 ,线段 交 轴于点 ,则 的值为 .(已知

如图,正方形 的对角线 上有一点 ,且 ,点 在 的延长线上,连接 ,过点 作 ,交 的延长线于点 ,连接 并延长,交 的延长线于点 ,若 , ,则线段 的长是 .

如图,直线 与 轴交于点 ,与 轴交于点 ,过点 作 ,交 轴于点 ,以 为边在 的右侧作正方形 ,延长 交 轴于点 ,以 为边在 的右侧作正方形 按照此规律继续作下去,再将每个正方形分割成四个全等的直角三角形和一个小正方形,每个小正方形的每条边都与其中的一条坐标轴平行,正方形 , , , 中的阴影部分的面积分别为 , , , ,则 可表示为 .
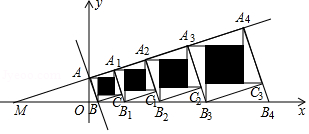
如图,射线 在第一象限,且与 轴正半轴的夹角为 ,过点 作 于点 ,作线段 的垂直平分线 交 轴于点 ,交 于点 ,作射线 ,以 为边在 的外侧作正方形 ,延长 交射线 于点 ,以 为边在 的外侧作正方形 ,延长 交射线 于点 ,以 为边在△ 的外侧作正方形 按此规律进行下去,则正方形 的周长为 .

我国魏晋时期的数学家刘徽创立了“割圆术”,认为圆内接正多边形边数无限增加时,周长就越接近圆周长,由此求得了圆周率 的近似值,设半径为 的圆内接正 边形的周长为 ,圆的直径为 ,如图所示,当 时, ,那么当 时, .(结果精确到0.01,参考数据:

试题篮
()