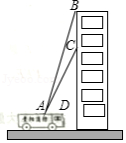
如图1,2分别是某款篮球架的实物图与示意图,已知底座 米,底座 与支架 所成的角 ,支架 的长为2.50米,篮板顶端 点到篮筐 的距离 米,篮板底部支架 与支架 所成的角 ,求篮筐 到地面的距离(精确到0.01米)(参考数据: , , , ,

某国发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作,如图,某探测队在地面 、 两处均探测出建筑物下方 处有生命迹象,已知探测线与地面的夹角分别是 和 ,且 米,求该生命迹象所在位置 的深度.(结果精确到1米,参考数据: , , ,

如图,吊车在水平地面上吊起货物时,吊绳 与地面保持垂直,吊臂 与水平线的夹角为 ,吊臂底部 距地面 .(计算结果精确到 ,参考数据 , ,
(1)当吊臂底部 与货物的水平距离 为 时,吊臂 的长为 .
(2)如果该吊车吊臂的最大长度 为 ,那么从地面上吊起货物的最大高度是多少?(吊钩的长度与货物的高度忽略不计)

贵阳市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在 处的求救者后,发现在 处正上方17米的 处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点 与居民楼的水平距离是15米,且在 点测得第一次施救时云梯与水平线的夹角 ,求第二次施救时云梯与水平线的夹角 的度数(结果精确到 ,可以使用科学计算器).
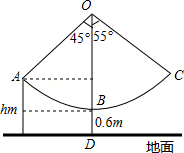
某新农村乐园设置了一个秋千场所,如图所示,秋千拉绳 的长为 ,静止时,踏板到地面距离 的长为 (踏板厚度忽略不计).为安全起见,乐园管理处规定:儿童的“安全高度”为 ,成人的“安全高度”为 (计算结果精确到
(1)当摆绳 与 成 夹角时,恰为儿童的安全高度,则
(2)某成人在玩秋千时,摆绳 与 的最大夹角为 ,问此人是否安全?(参考数据: , , ,

某新农村乐园设置了一个秋千场所,如图所示,秋千拉绳 的长为 ,静止时,踏板到地面距离 的长为 (踏板厚度忽略不计).为安全起见,乐园管理处规定:儿童的“安全高度”为 ,成人的“安全高度”为 (计算结果精确到
(1)当摆绳 与 成 夹角时,恰为儿童的安全高度,则
(2)某成人在玩秋千时,摆绳 与 的最大夹角为 ,问此人是否安全?(参考数据: , , ,
阅读材料:关于三角函数还有如下的公式:
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值.
例:
根据以上阅读材料,请选择适当的公式解答下面问题
(1)计算: ;
(2)某校在开展爱国主义教育活动中,来到烈士纪念碑前缅怀和纪念为国捐躯的红军战士.李三同学想用所学知识来测量如图纪念碑的高度.已知李三站在离纪念碑底7米的 处,在 点测得纪念碑碑顶的仰角为 , 为 米,请你帮助李三求出纪念碑的高度.

据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过 ,在一条笔直公路 的上方 处有一探测仪,如平面几何图, , ,第一次探测到一辆轿车从 点匀速向 点行驶,测得 ,2秒后到达 点,测得 , ,结果精确到
(1)求 , 的距离.
(2)通过计算,判断此轿车是否超速.

如图,某武警部队在一次地震抢险救灾行动中,探险队员在相距4米的水平地面 , 两处均探测出建筑物下方 处有生命迹象,已知在 处测得探测线与地面的夹角为 ,在 处测得探测线与地面的夹角为 ,求该生命迹象 处与地面的距离.(结果精确到0.1米,参考数据: ,

“ ”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中 , , ,请根据图中数据,求出线段 和 的长. , , ,结果保留小数点后一位)

图①是放置在水平面上的台灯,图②是其侧面示意图(台灯底座高度忽略不计),其中灯臂 ,灯罩 ,灯臂与底座构成的 . 可以绕点 上下调节一定的角度.使用发现:当 与水平线所成的角为 时,台灯光线最佳.现测得点 到桌面的距离为 .请通过计算说明此时台灯光线是否为最佳?(参考数据: 取 .

某数学课题研究小组针对兰州市住房窗户“如何设计遮阳蓬”这一课题进行了探究,过程如下:
问题提出:
如图1是某住户窗户上方安装的遮阳蓬,要求设计的遮阳蓬能最大限度地遮住夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内.

方案设计:
如图2,该数学课题研究小组通过调查研究设计了垂直于墙面 的遮阳蓬 .
数据收集:
通过查阅相关资料和实际测量:兰州市一年中,夏至日这一天的正午时刻太阳光线 与遮阳蓬 的夹角 最大 ;冬至日这一天的正午时刻,太阳光线 与遮阳蓬 的夹角 最小 .窗户的高度 .
问题解决:
根据上述方案及数据,求遮阳蓬 的长.
(结果精确到 ,参考数据: , , , , ,
如图,某城市市民广场一入口处有五级高度相等的小台阶.已知台阶总高1.5米,为了安全,现要做一个不锈钢扶手 及两根与 垂直且长为1米的不锈钢架杆 和 (杆子的底端分别为 、 ,且 .(参考数据: ,
(1)求点 与点 的高度差 ;
(2)求所有不锈钢材料的总长度(即 的长,结果精确到0.1米)

试题篮
()