初中数学加权平均数试题

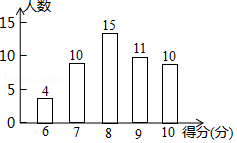
为了了解居民的环保意识，社区工作人员在光明小区随机抽取了若干名居民开展主题为“打赢蓝天保卫战”的环保知识有奖问答活动，并用得到的数据绘制了如图条形统计图（得分为整数，满分为10分，最低分为6分）

请根据图中信息，解答下列问题：

（1）本次调查一共抽取了　　名居民；

（2）求本次调查获取的样本数据的平均数、众数和中位数；

（3）社区决定对该小区500名居民开展这项有奖问答活动，得10分者设为“一等奖”，请你根据调查结果，帮社区工作人员估计需准备多少份“一等奖”奖品？

今年我市将创建全国森林城市，提出了“共建绿色城”的倡议．某校积极响应，在3月12日植树节这天组织全校学生开展了植树活动，校团委对全校各班的植树情况进行了统计，绘制了如图所示的两幅不完整的统计图．

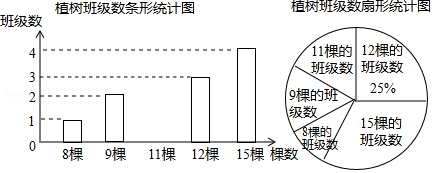
（1）求该校的班级总数；

（2）将条形统计图补充完整；

（3）求该校各班在这一活动中植树的平均棵树．

某校为选拔一名选手参加“美丽邵阳，我为家乡做代言”主题演讲比赛，经研究，按图所示的项目和权数对选拔赛参赛选手进行考评（因排版原因统计图不完整）．下表是李明、张华在选拔赛中的得分情况：

项目 选手	服装	普通话	主题	演讲技巧
李明	85	70	80	85
张华	90	75	75	80

结合以上信息，回答下列问题：

（1）求服装项目的权数及普通话项目对应扇形的圆心角大小；

（2）求李明在选拔赛中四个项目所得分数的众数和中位数；

（3）根据你所学的知识，帮助学校在李明、张华两人中选择一人参加“美丽邵阳，我为家乡做代言”主题演讲比赛，并说明理由．

某校组织学生参加植树活动，活动结束后，统计了九年级甲班50名学生每人植树的情况，绘制了如下的统计表：

植树棵数	3	4	5	6
人数	20	15	10	5

那么这50名学生平均每人植树　　棵．

为提高节水意识， 小申随机统计了自己家 7 天的用水量， 并分析了第 3 天的用水情况， 将得到的数据进行整理后， 绘制成如图所示的统计图 ． （单 位： 升）

（1） 求这 7 天内小申家每天用水量的平均数和中位数；

（2） 求第 3 天小申家洗衣服的水占这一天总用水量的百分比；

（3） 请你根据统计图中的信息， 给小申家提出一条合理的节约用水建议， 并估算采用你的建议后小申家一个月 （按 30 天计算） 的节约用水量 ．

湖南省2017年公务员录用考试是这样统计成绩的，综合成绩 $=$笔试成绩 $\times 60\%+$面试成绩 $\times 40\%$，小红姐姐的笔试成绩是82分，她的竞争对手的笔试成绩是86分，小红姐姐要使自己的综合成绩追平竞争对手，则她的面试成绩必须比竞争对手多 $($　　 $)$

A．2.4分B．4分C．5分D．6分

在6.26国际禁毒日到来之际，贵阳市教育局为了普及禁毒知识，提高禁毒意识，举办了“关爱生命，拒绝毒品”的知识竞赛．某校初一、初二年级分别有300人，现从中各随机抽取20名同学的测试成绩进行调查分析，成绩如下：

初一：	68	88	100	100	79	94	89	85	100	88
	100	90	98	97	77	94	96	100	92	67
初二：	69	97	96	89	98	100	99	100	95	100
	99	69	97	100	99	94	79	99	98	79

（1）根据上述数据，将下列表格补充完成．

整理、描述数据：

分数段	$60⩽x⩽69$	$70⩽x⩽79$	$80⩽x⩽89$	$90⩽x⩽100$
初一人数	2	2	4	12
初二人数	2	2	1	15

分析数据：样本数据的平均数、中位数、满分率如表：

年级	平均数	中位数	满分率
初一	90.1	93	$25\%$
初二	92.8		$20\%$

得出结论：

（2）估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共　　人；

（3）你认为哪个年级掌握禁毒知识的总体水平较好，说明理由．

贵阳市“阳光小区”开展“节约用水，从我做起”的活动，一个月后，社区居委会从小区住户中抽取10个家庭与他们上个月的用水量进行比较，统计出节水情况如表：

节水量 $\left(m^3\right)$	0.3	0.4	0.5	0.6	0.7
家庭数（个 $)$	2	2	4	1	1

那么这10个家庭的节水量 $\left(m^3\right)$的平均数和中位数分别是 $($　　 $)$

A．0.47和0.5B．0.5和0.5C．0.47和4D．0.5和4

某校九年级（1）班全体学生2016年初中毕业体育考试的成绩统计如表：

成绩（分 $)$	35	39	42	44	45	48	50
人数（人 $)$	2	5	6	6	8	7	6

根据表中的信息判断，下列结论中错误的是 $($　　 $)$

A．该班一共有40名同学

B．该班学生这次考试成绩的众数是45分

C．该班学生这次考试成绩的中位数是45分

D．该班学生这次考试成绩的平均数是45分

今年5月13日是“母亲节”，某校开展“感恩母亲，做点家务”活动为了了解同学们在母亲节这一天做家务情况，学校随机抽查了部分同学，并用得到的数据制成如下不完整的统计表：

做家务时间（小时）	人数	所占百分比
$A$组：0.5	15	$30\%$
$B$组：1	30	$60\%$
$C$组：1.5	$x$	$4\%$
$D$组：2	3	$6\%$
合计	$y$	$100\%$

（1）统计表中的 $x=$　　， $y=$　　；

（2）小君计算被抽查同学做家务时间的平均数是这样的：

第一步：计算平均数的公式是 $\bar{x}=\frac{x_1+x_2+x_3+\dots +x_n}{n}$，

第二步：该问题中 $n=4$， $x_1=0.5$， $x_2=1$， $x_3=1.5$， $x_4=2$，

第三步： $\bar{x}=\frac{0.5+1+1.5+2}{4}=1.25$（小时）

小君计算的过程正确吗？如果不正确，请你计算出正确的做家务时间的平均数；

（3）现从 $C$， $D$两组中任选2人，求这2人都在 $D$组中的概率（用树形图法或列表法）．

红树林学校在七年级新生中举行了全员参加的“防溺水”安全知识竞赛，试卷题目共10题，每题10分．现分别从三个班中各随机取10名同学的成绩（单位：分），收集数据如下：

1班：90，70，80，80，80，80，80，90，80，100；

2班：70，80，80，80，60，90，90，90，100，90；

3班：90，60，70，80，80，80，80，90，100，100．

整理数据：

分数 人数 班级	60	70	80	90	100
1班	0	1	6	2	1
2班	1	1	3	$a$	1
3班	1	1	4	2	2

分析数据：

	平均数	中位数	众数
1班	83	80	80
2班	83	$c$	$d$
3班	$b$	80	80

根据以上信息回答下列问题：

（1）请直接写出表格中 $a$， $b$， $c$， $d$的值；

（2）比较这三组样本数据的平均数、中位数和众数，你认为哪个班的成绩比较好？请说明理由；

（3）为了让学生重视安全知识的学习，学校将给竞赛成绩满分的同学颁发奖状，该校七年级新生共570人，试估计需要准备多少张奖状？

为弘扬传统文化，某校开展了“传承经典文化，阅读经典名著”活动．为了解七、八年级学生（七、八年级各有600名学生）的阅读效果，该校举行了经典文化知识竞赛．现从两个年级各随机抽取20名学生的竞赛成绩（百分制）进行分析，过程如下：

收集数据：

七年级：79，85，73，80，75，76，87，70，75，94，75，79，81，71，75，80，86，59，83，77．

八年级：92，74，87，82，72，81，94，83，77，83，80，81，71，81，72，77，82，80，70，41．

整理数据：

	$40⩽x⩽49$	$50⩽x⩽59$	$60⩽x⩽69$	$70⩽x⩽79$	$80⩽x⩽89$	$90⩽x⩽100$
七年级	0	1	0	$a$	7	1
八年级	1	0	0	7	$b$	2

分析数据：

	平均数	众数	中位数
七年级	78	75	$c$
八年级	78	$d$	80.5

应用数据：

（1）由上表填空： $a=$　　， $b=$　　， $c=$　　， $d=$　　．

（2）估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人？

（3）你认为哪个年级的学生对经典文化知识掌握的总体水平较好，请说明理由．

为了解某校八年级学生一门课程的学习情况，小佳和小丽分别对八年级1班和2班本门课程的期末成绩进行了调查分析．

小佳对八年级1班全班学生 $(25$名）的成绩进行分析，过程如下：

收集、整理数据：

表一

分数段 班级	$60⩽x<70$	$70⩽x<80$	$80⩽x<90$	$90⩽x⩽100$
八年级1班	7	5	10	3

分析数据：

表二

统计量 班级	平均数	中位数	众数	极差	方差
八年级1班	78		85	36	105.28

小丽用同样的方法对八年级2班全班学生 $(25$名）的成绩进行分析，数据如下：

表三

统计量 班级	平均数	中位数	众数	极差	方差
八年级2班	75	76	73	44	146.80

根据以上信息，解决下列问题：

（1）已知八年级1班学生的成绩在 $80⩽x<90$这一组的数据如下：

85，87，88，80，82，85，83，85，87，85

根据上述数据，将表二补充完整；

（2）你认为哪个班级的成绩更为优异？请说明理由．

甲乙两人进行射击训练，两人分别射击12次，如图分别统计了两人的射击成绩，已知甲射击成绩的方差 $S_{甲}^2=\frac{7}{12}$，平均成绩 $\overline{x_{甲}}=8.5$．

（1）根据图上信息，估计乙射击成绩不少于9环的概率是多少？

（2）求乙射击的平均成绩的方差，并据此比较甲乙的射击“水平”．

$S^2=\frac{1}{n}[{(x_1-\bar{x})}^2+{(x_2-\bar{x})}^2\dots {(x_n-\bar{x})}^2]$．

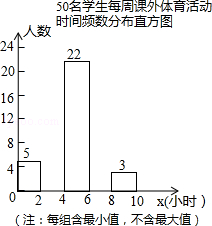
为增强学生体质，各学校普遍开展了阳光体育活动，某校为了解全校1000名学生每周课外体育活动时间的情况，随机调查了其中的50名学生，对这50名学生每周课外体育活动时间 x（单位：小时）进行了统计．根据所得数据绘制了一幅不完整的统计图，并知道每周课外体育活动时间在6≤ x＜8小时的学生人数占24%．根据以上信息及统计图解答下列问题：

（1）本次调查属于 　　调查，样本容量是 　　；

（2）请补全频数分布直方图中空缺的部分；

（3）求这50名学生每周课外体育活动时间的平均数；

（4）估计全校学生每周课外体育活动时间不少于6小时的人数．