初中数学列表法与树状图法试题

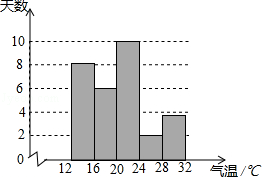
为了解某地某个季度的气温情况，用适当的抽样方法从该地这个季度中抽取30天，对每天的最高气温 x（单位：℃）进行调查，并将所得的数据按照12≤ x＜16，16≤ x＜20，20≤ x＜24，24≤ x＜28，28≤ x＜32分成五组，得到如图频数分布直方图．

（1）求这30天最高气温的平均数和中位数（各组的实际数据用该组的组中值代表）；

（2）每月按30天计算，各组的实际数据用该组的组中值代表，估计该地这个季度中最高气温超过（1）中平均数的天数；

（3）如果从最高气温不低于24℃的两组内随机选取两天，请你直接写出这两天都在气温最高一组内的概率．

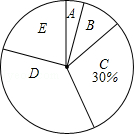
鄂尔多斯市加快国家旅游改革先行示范区建设，越来越多的游客慕名而来，感受鄂尔多斯市"24℃夏天的独特魅力"，市旅游局工作人员依据2016年7月份鄂尔多斯市各景点的游客数量，绘制了如下尚不完整的统计图；

根据以上信息解答下列问题：

（1）2016年7月份，鄂尔多斯市共接待游客 　 　万人，扇形统计图中乌兰木伦景观湖所对应的圆心角的度数是 　 　，并补全条形统计图；

（2）预计2017年7月份约有200万人选择来鄂尔多斯市旅游，通过计算预估其中选择去响沙湾旅游的人数；

（3）甲、乙两个旅行团准备去响沙湾、成吉思汗陵、蒙古源流三个景点旅游，若这三个景点分别记作 a、 b、 c，请用树状图或列表法求他们选择去同一个景点的概率．

为了增强中学生的体质，某校食堂每天都为学生提供一定数量的水果，学校李老师为了了解学生喜欢吃哪种水果，进行了抽样调查，调查分为五种类型： A．喜欢吃苹果的学生； B．喜欢吃桔子的学生； C．喜欢吃梨的学生； D．喜欢吃香蕉的学生； E．喜欢吃西瓜的学生，并将调查结果绘制成图1和图2的统计图（不完整）．请根据图中提供的数据解答下列问题：

（1）求此次抽查的学生人数；

（2）将图2补充完整，并求图1中的 x；

（3）现有5名学生，其中 A类型3名， B类型2名，从中任选2名学生参加体能测试，求这两名学生为同一类型的概率（用列表法或树状图法）

有三张正面分别标有数字﹣3，1，3的不透明卡片，它们除数字外都相同，现将它们背面朝上，洗匀后从三张卡片中随机地抽取一张，放回卡片洗匀后，再从三张卡片中随机地抽取一张．

（1）试用列表或画树状图的方法，求两次抽取的卡片上的数字之积为负数的概率；

（2）求两次抽取的卡片上的数字之和为非负数的概率．

某卫视曾播出一期"辨脸识人"节目，参赛选手以家庭为单位，每组家庭由爸爸、妈妈和宝宝组成，爸爸、妈妈和宝宝分散在三块区域，选手需在宝宝中选一个宝宝，然后分别在爸爸区域和妈妈区域中正确找出这个宝宝的父母，不考虑其他因素，仅数学角度思考，已知在某期比赛中有 A、 B、 C、 D四组家庭进行比赛．

（1）选手选择 A组家庭的宝宝，在妈妈区域中正确找出其妈妈的概率是多少？

（2）如果任选一个宝宝（假如选 A组家庭），通过列表或画树形图的方法，求选手至少正确找对宝宝父母其中一人的概率．

某卫视曾播出一期“辨脸识人”节目，参赛选手以家庭为单位，每组家庭由爸爸、妈妈和宝宝组成，爸爸、妈妈和宝宝分散在三块区域，选手需在宝宝中选一个宝宝，然后分别在爸爸区域和妈妈区域中正确找出这个宝宝的父母，不考虑其他因素，仅数学角度思考，已知在某期比赛中有A、B、C、D四组家庭进行比赛．

（1）选手选择A组家庭的宝宝，在妈妈区域中正确找出其妈妈的概率是多少？

（2）如果任选一个宝宝（假如选A组家庭），通过列表或画树形图的方法，求选手至少正确找对宝宝父母其中一人的概率．

有甲、乙两个不透明的布袋，甲袋中有2个完全相同的小球，分别标有数字0和﹣2；乙袋中有3个完全相同的小球，分别标有数字﹣2，0和1，小明从甲袋中随机取出1个小球，记录标有的数字为 x，再从乙袋中随机取出1个小球，记录标有的数字为 y，这样确定了点 Q的坐标（ x， y）

（1）写出先 Q所有可能的坐标；

（2）求点 Q在 x轴上的概率．

一个不透明的口袋中装有4个球，分别是红球和白球，这些球除颜色外都相同，将球搅匀，先从中任意摸出一个球，恰好摸到红球的概率等于 $\frac{1}{2}$ ．

（1）求口袋中有几个红球？

（2）先从中任意摸出一个球，从余下的球中再摸出一个球，请用列表法或树状图法求两次摸到的球中一个是红球和一个是白球的概率．

今年5月份，某校九年级学生参加了鄂尔多斯市中考体育考试，为了了解该校九年级（1）班学生的中考体育情况，对全班学生的中考体育成绩进行了统计，并绘制出以下不完整的频数分布表和扇形统计图，请根椐图表中的信息解答下列问题：

分组	分数段（分）	频数
A	8≤ x＜10.5	2
B	10.5≤ x＜13	5
C	13≤ x＜15.5	15
D	15.5≤ x＜18	m
E	18≤ x＜20.5	10

（1）九年级（1）班学生人数为 　 　人， m＝ 　 　．

（2）该班学生中考体育成绩的中位数落在 　 　分数段，扇形统计图中 E组所对应扇形的圆心角的度数是 　 　．

（3）该班中考体育成绩满分（20分）共有4人，其中男生2人，女生2人，现需从4人中随机选取2人到八年级进行经验交流，请用"列表法"或"画树状图法"，求出恰好选到一男一女的概率．

下表是博文学校初三•一班慧慧、聪聪两名学生入学以来10次数学检测成绩（单位：分）．

慧慧	116	124	130	126	121	127	126	122	125	123
聪聪	122	124	125	128	119	120	121	128	114	119

回答下列问题：

（1）分别求出慧慧和聪聪成绩的平均数；

（2）分别计算慧慧和聪聪两组数据的方差；

（3）根据（1）（2）你认为选谁参加全国数学竞赛更合适？并说明理由；

（4）由于初三•二班、初三•三班和初三•四班数学成绩相对薄弱，学校打算派慧慧和聪聪分别参加三个班的数学业余辅导活动，求两名学生分别在初三•二班和初三•三班的概率．

从数字2，3，4中任选两个数组成一个两位数，组成的数是偶数的概率是（　　）

A．

$\frac{2}{3}$

B．

$\frac{1}{2}$

C．

$\frac{1}{3}$

D．

$\frac{5}{6}$

张老师为了解所教班级学生完成数学课前预习的具体情况，对本班部分学生进行了为期半个月的跟踪调查，他将调查结果分为四类， A：很好； B：较好； C：一般； D：较差．并将调查结果绘制成以下两幅不完整的统计图，请你根据统计图解答下列问题：

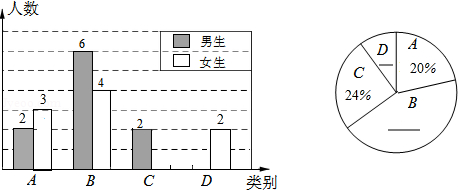
（1）张老师一共调查了多少名同学？

（2） C类女生有多少名？ D类男生有多少名？并将两幅统计图补充完整；

（3）为了共同进步，张老师想从被调查的 A类和 D类学生中各随机选取一位学生进行"一帮一"互助学习，请用列表法或画树状图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率．

近年来，我国持续的大面积的雾霾天气让环境和健康问题成为焦点，为了调查学生对雾霾天气知识的了解程度，某校在学生中做了一次抽样调查，调查结果共分为四个等级：A．非常了解；B．比较了解；C．基本了解；D．不了解．根据调查统计结果，绘制了如图所示的不完整的三种统计图表．

对雾霾所了解程度的统计表：

对雾霾的了解程度	百分比
A．非常了解	5%
A．比较了解	15%
C．基本了解	45%
D．不了解	n

请结合统计图表，回答下列问题：

（1）本次参与调查的学生共有　　人，n＝　　；

（2）扇形统计图中D部分扇形所对应的圆心角是　　度；

（3）请补全条形统计图；

（4）根据调查结果，学校准备开展关于雾霾的知识竞赛，某班要从“非常了解”程度的小明和小刚中选一人参加，现设计了如下游戏来确定，具体规则是：把四个完全相同的乒乓球标上数字1，2，3，4，然后放到一个不透明的袋中，一个人先从袋中随机摸出一个球，另一人再从剩下的三个球中随机摸出一个球．若摸出的两个球上的数字和为奇数，则小明去，否则小刚去．请用树状图或列表法说明这个游戏规则是否公平．

在甲、乙两个不透明的布袋里，都装有3个大小、材质完全相同的小球，其中甲袋中的小球上分别标有数字0，1，2；乙袋中的小球上分别标有数字﹣1，﹣2，0．现从甲袋中任意摸出一个小球，记其标有的数字为x，再从乙袋中任意摸出一个小球，记其标有的数字为y，以此确定点M的坐标（x，y）．

（1）请你用画树状图或列表的方法，写出点M所有可能的坐标；

（2）求点M（x，y）在函数 $y=-\frac{2}{x}$的图象上的概率．

小明和小军两人一起做游戏，游戏规则如下：每人从1，2，…，8中任意选择一个数字，然后两人各转动一次如图所示的转盘（转盘被分为面积相等的四个扇形），两人转出的数字之和等于谁事先选择的数，谁就获胜；若两人转出的数字之和不等于他们各自选择的数，就在做一次上述游戏，直至决出胜负．若小军事先选择的数是5，用列表或画树状图的方法求他获胜的概率．