初中数学利用频率估计概率选择题

在一个不透明的口袋中放着红色、黑色、黄色的橡皮球共有30个，它们除颜色外其它全相同．小刚通过多次摸球试验后发现从中摸到红色球或黄色球的频率稳定在0.15和0.45之间，则口袋中黑色球的个数可能是 （   ）                 

A．14

B．20

C．9

D．6

一只小鸟自由自在地在空中飞行，然后随意落在如图所示的某个方格中（每个方格除颜色外完全一样），那么小鸟停在黑色方格中的概率是（  ）

A．

B．

C．

D．

气象台预测“本市降雨的概率是80%”，对预测的正确理解是
A、本市明天有80%的地区降雨；    B、本市明天将有80%的时间降雨；
C、明天出行不带雨具会淋雨；      D、明天出行不带雨具肯定会淋雨．

以下说法合理的是（ ）

A．小明在10次抛图钉的试验中发现3次钉尖朝上，由此他说钉尖朝上的概率是30%

B．抛掷一枚普通的正六面体骰子，出现6的概率是的意思是每6次就有1次掷得6

C．某彩票的中奖机会是2%，那么如果买100张彩票一定会有2张中奖。

D．在一次课堂进行的试验中，甲、乙两组同学估计硬币落地后，正面朝上的概率分别为0．48和0．51。

若自然数使得三个数的加法运算“”产生进位现象，则称为“连加进位数”．例如，2不是“连加进位数”，因为不产生进位现象；4是“连加进位数”，因为产生进位现象；51是“连加进位数”，因为产生进位现象．如果从0，1，…，99这100个自然数中任取一个数，那么取到“连加进位数”的概率是（　 　）。

A．0.91

B．0.90

C．0.89

D．0.88

假定鸟卵孵化后，雏鸟为雌与雄的概率相同．如果三枚卵全部成功孵化，则三只雏鸟中恰有两只雌鸟的概率是

A．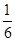

B．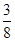

C．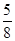

D．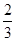

下列说法中，正确的是（ ）

A．在同一年出生的367名学生中，至少有两人的生日是同一天

B．“抛一枚硬币正面朝上的概率是0．5”表示每抛硬币2次就有1次出现正面朝上

C．“彩票中奖的概率是1%”表示买100张彩票一定有1张会中奖

D．“明天降雨的概率是80％”表示明天有80％的时间降雨

给甲、乙、丙三人打电话，若打电话的顺序是任意的，则第一个打电话给甲的概率为（    ）

A．

B．

C．

D．

下列事件中，必然事件是（ ）

A．掷一枚硬币，正面朝上

B．任意三条线段可以组成一个三角形

C．投掷一枚质地均匀的骰子，掷得的点数是奇数

D．抛出的篮球会下落

下列事件中，必然事件是（   ）

A．掷一枚硬币，着地时反面向上

B．星期天一定是晴天

C．打开电视机，正在播放动画片

D．在标准大气压下，水加热到100°会沸腾

下列事件中，是确定事件的有（   ）

A．打开电视，正在播放广告

B．三角形三个内角的和是180°

C．两个负数的和是正数

D．某名牌产品一定是合格产品

小张抛一枚质地均匀的硬币，出现正面朝上的可能性是（ ）

A．25%

B．50%

C．75%

D．85%

盒子里有完全相同的三个小球，球上分别标有数字-2，1，4．随机摸出一个小球，其数字为p（放回），再随机摸出一个小球，其数字记为q，则满足关于x的方程x²＋px＋q=0有实数根的概率是（   ）.

A．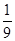

B．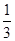

C．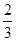

D．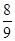

袋子中装有4个黑球和2个白球，这些球的形状、大小、质地等完全相同，在看不到球的条件下，随机地从袋子中摸出三个球．下列事件是必然事件的是（   ）

A．摸出的三个球中至少有一个球是黑球

B．摸出的三个球中至少有一个球是白球

C．摸出的三个球中至少有两个球是黑球

D．摸出的三个球中至少有两个球是白球

现有A、B两枚均匀的小立方体（立方体的每个面上分别标有1、2、3、4、5、6），甲同学掷A立方体朝上的数字记为x，乙同学掷B立方体朝上的数字记为y，现用x、y来确定点P（x,y），那么他们各掷一次确定的点P落在已知直线上的概率为（    ）   
A．     B．   C．   D．