下列说法错误的是
| A. |
必然事件发生的概率是1 |
| B. |
通过大量重复试验,可以用频率估计概率 |
| C. |
概率很小的事件不可能发生 |
| D. |
投一枚图钉,"钉尖朝上"的概率不能用列举法求得 |
为了解某地区九年级男生的身高情况,随机抽取了该地区100名九年级男生,他们的身高 统计如下:
| 组别 |
|
|
|
|
| 人数 |
5 |
38 |
42 |
15 |
根据以上结果,抽查该地区一名九年级男生,估计他的身高不低于 的概率是
| A. |
0.85 |
B. |
0.57 |
C. |
0.42 |
D. |
0.15 |
一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有9个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球实验后发现,摸到黄球的频率稳定在30%,那么估计盒子中小球的个数n为( )
A.20B.24C.28D.30
为了解某地区九年级男生的身高情况,随机抽取了该地区1000名九年级男生的身高数据,统计结果如下:
| 身高 |
|
|
|
|
| 人数 |
60 |
260 |
550 |
130 |
根据以上统计结果,随机抽取该地区一名九年级男生,估计他的身高不低于 的概率是
| A. |
0.32 |
B. |
0.55 |
C. |
0.68 |
D. |
0.87 |
甲、乙两名同学在一次用频率去估计概率的实验中,统一了某一结果出现的频率绘出的统计图 如图所示,则符合这一结果的实验可能是( )

| A.从一个装有2个白球和1个红球的袋子中任取两球,取到两个白球的概率 |
| B.任意写一个正整数,它能被 2 整除的概率 |
| C.抛一枚硬币,连续两次出现正面的概率 |
| D.掷一枚正六面体的骰子,出现 1 点的概率 |
在课外实践活动中,甲、乙、丙、丁四个小组用投掷一元硬币的方法估算正面朝上的概率,其实验次数分别为10次、50次、100次,200次,其中实验相对科学的是( )
A.甲组B.乙组C.丙组D.丁组
下列说法错误的是
| A. |
必然事件发生的概率为1 |
| B. |
平均数和方差都不易受极端值的影响 |
| C. |
抽样调查抽取的样本是否具有代表性,直接关系对总体估计的准确程度 |
| D. |
可以通过大量重复试验,用一个随机事件发生的频率去估计它的概率 |
一个不透明的袋子中有红球、白球共20个这些球除颜色外都相同将袋子中的球搅匀后,从中随意摸出1个球,记下颜色后放回,不断重复这个过程,共摸了100次,其中有30次摸到红球,由此可以估计袋子中红球的个数约为
A.12B.10C.8D.6
如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.
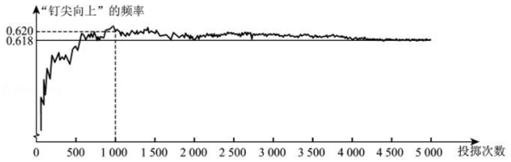
下面有三个推断:
①当投掷次数是500时,计算机记录"钉尖向上"的次数是308,所以"钉尖向上"的概率是0.616;
②随着试验次数的增加,"钉尖向上"的频率总在0.618附近摆动,显示出一定的稳定性,可以估计"钉尖向上"的概率是0.618;
③若再次用计算机模拟此实验,则当投掷次数为1000时,"钉尖向上"的频率一定是0.620.
其中合理的是
| A. |
① |
B. |
② |
C. |
①② |
D. |
①③ |
某学习小组做"用频率估计概率"的试验时,统计了某一结果出现的频率,绘制了如下折线统计图,则符合这一结果的试验最有可能的是( )

| A. |
袋中装有大小和质地都相同的3个红球和2个黄球,从中随机取一个,取到红球 |
| B. |
掷一枚质地均匀的正六面体骰子,向上的面的点数是偶数 |
| C. |
先后两次掷一枚质地均匀的硬币,两次都出现反面 |
| D. |
先后两次掷一枚质地均匀的正六面体骰子,两次向上的面的点数之和是7或超过9 |
小明和同学做“抛掷质地均匀的硬币试验”获得的数据如表:
抛掷次数 |
100 |
200 |
300 |
400 |
500 |
正面朝上的频数 |
53 |
98 |
156 |
202 |
244 |
若抛掷硬币的次数为1000,则“正面朝上”的频数最接近
A.20B.300C.500D.800
在6张完全相同的卡片上分别画上线段、等边三角形、平行四边形、圆、正方形、直角梯形,在看不见图形的情况下随机摸出1张,这张卡片上的图形既是中心对称图形又是轴对称图形的概率是( )
A. |
B. |
C.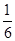 |
D. |
某小组做“用频率估计概率”的试验时,绘出的某一结果出现的频率折线图,则符合这一结果的试验可能是

A.抛一枚硬币,出现正面朝上
B.掷一个正六面体的骰子,出现3点朝上
C.一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D.从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
某射击运动员在同一条件下的射击成绩记录如下:
| 射击次数 |
20 |
80 |
100 |
200 |
400 |
1000 |
| "射中九环以上"的次数 |
18 |
68 |
82 |
168 |
327 |
823 |
| "射中九环以上"的频率(结果保留两位小数) |
0.90 |
0.85 |
0.82 |
0.84 |
0.82 |
0.82 |
根据频率的稳定性,估计这名运动员射击一次时"射中九环以上"的概率约是
| A. |
0.90 |
B. |
0.82 |
C. |
0.85 |
D. |
0.84 |
一个布袋里有6只颜色不同的球,其中2个红球,4个白球,从布袋里任意摸出一个球,则摸出的球的红球的概率为( )
A. |
B.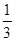 |
C.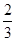 |
D. |
试题篮
()