初中数学利用频率估计概率解答题

经过某十字路口的汽车，它可能继续直行，也可能向左转或向右转．
（1）如果这三种情况是等可能的，当三辆汽车经过这个十字路口时，求三辆车全部同向而行的概率；
（2）交管部门在汽车行驶高峰时段对车流量作了统计，发现汽车在此十字路口直行的频率为，向左转和向右转的频率均为．目前在此路口，汽车左转、右转、直行的绿灯亮的时间均为30秒，在绿灯亮总时间不变的条件下，为了缓解交通拥挤，请你对此路口三个方向的绿灯亮的时间做出合理的调整．

如图，依据闯关游戏规则，请你探究“闯关游戏”的奥秘：

（1）用列表的方法表示有可能的闯关情况；
（2）求出闯关成功的概率.

如图，有四张背面相同的纸牌A、B、C、D，其正面分别是红桃、方块、黑桃、梅花，其中红桃、方块为红色，黑桃、梅花为黑色．小明将这4张纸牌背面朝上洗匀后，摸出一张，将剩余3张再摸出一张．

（1）用树状图（或列表法）表示两次摸牌所有可能出现的结果（纸牌用A，B，C，D表示）；
（2）求摸出的两张牌同为红色的概率．

有四张形状、大小和质地相同的卡片A、B、C、D，正面分别写有一个正多边形（所有正多边形的边长相等），把四张卡片洗匀后正面朝下放在桌面上，从中随机抽取一张（不放回），接着再随机抽取一张．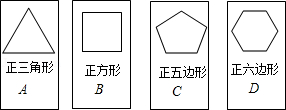

（1）请你用画树形图或列表的方法列举出可能出现的所有结果；
（2）如果在（1）中各种结果被选中的可能性相同，求两次抽取的正多边形能构成平面镶嵌的概率；
（3）若两种正多边形构成平面镶嵌，p、q表示这两种正多边形的个数，x、y表示对应正多边形的每个内角的度数，则有方程px＋qy＝360，求每种平面镶嵌中p、q的值．

小丽和小华想利用摸球游戏决定谁去参加市里举办的书法比赛,游戏规则是:在一个不透明的袋子里装有除数字外完全相同的4个小球,上面分别标有数字2,3,4,5.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为偶数,则小丽去参赛;否则小华去参赛.
（1）用列表法或画树状图法,求小丽参赛的概率.
（2）你认为这个游戏公平吗?请说明理由.

有三张卡片（背面完全相同）分别写有，1，2把它们背面朝上洗匀后，小军从中抽取一张，记下这个数后放回洗匀，小明又从中抽出一张。
（1）两人抽取的卡片上的数都是1的概率是多少？
（2）李刚为他们俩设定了一个游戏规则：若两人抽取的卡片上两数之积是有理数，则小军胜；否则小明获胜，你认为这个游戏规则对谁有利？请用画树状图的方法进行分析说明．

不透明的口袋里装有红、黄、蓝三种颜色的小球（除颜色不同外，其它都一样），其中红球2个，蓝球1个，现在从中任意摸出一个红球的概率为.
（1）求袋中黄球的个数；
（2）第一次摸出一个球（不放回），第二次再摸出一个球，请用树状图或列表法求两次摸出的都是红球的概率.

（本题10分）某校九年级举行毕业典礼，需要从九（1）班的2名男生1名女生、九（2）的1
名男生1名女生共5人中选出2名主持人．
（1）用树形图或列表法列出所有可能情形；
（2）求2名主持人来自不同班级的概率；
（3）求2名主持人恰好1男1女的概率．

将如图所示的牌面数字分别是1，2，3，4的四张扑克牌背面朝上，洗匀后放在桌面上．

（1）从中随机抽出一张牌，牌面数字是偶数的概率是        ；
（2）从中随机抽出二张牌，两张牌牌面数字的和是5的概率是       ；
（3）先从中随机抽出一张牌，将牌面数字作为十位上的数字，然后将该牌放回并重新洗匀，再随机抽取一张，将牌面数字作为个位上的数字，请用画树状图或列表的方法求组成的两位数恰好是4的倍数的概率．

把大小和形状完全相同的6张卡片分成两组，每组3张，分别标上数字1、2、3，将这两组卡片分别放入两个盒子中搅匀，再从中各随机投取一张．
（1）试求取出的两张卡片数字之和为奇数概率；
（2）若取出的两张卡片数字之和为奇数，则甲胜；取出的两张卡片数字之和为偶数，则乙胜；试分析这个游戏是否公平？请说明理由．

已知甲同学手中藏有三张分别标有数字，，1的卡片，乙同学手中藏有三张分别标有数字1，3，2的卡片，卡片外形相同，现从甲乙两人手中各任取一张卡片，并将它们的数字分别记为，．
(1)请你用树形图或列表法列出所有可能的结果．
(2)现制定这样一个游戏规则：若所选出的，能使得有两个不相等的实数根，则甲获胜；否则乙获胜．请问这样的游戏规则公平吗？请你用概率知识解释．

一个口袋中有4个相同的小球，分别与写有字母A，B，C，D，随机地抽出一个小球后放回，再随机地抽出一个小球．
（1）使用列表法或画树状图法中的一种，列举出两次抽出的球上字母的所有可能结果；
（2）求两次抽出的球上字母相同的概率．

请你依据右面图框中的寻宝游戏规则，探究“寻宝游戏”的奥秘：
 
⑴用树状图表示出所有可能的寻宝情况；
⑵求在寻宝游戏中胜出的概率.

（本题8分）在一个不透明的口袋里装有若干个质地相同的红球, 为了估计袋中红球的数量，某学习小组做了摸球实验, 他们将30个与红球大小形状完全相同的白球装入袋中，搅匀后从中随机摸出一个球并记下颜色, 再把它放回袋中, 多次重复摸球. 下表是多次活动汇总后统计的数据：

摸球的次数S	150	200	500	900	1000	1200
摸到白球的频数n	51	64	156	275	303	361
摸到白球的频率	0.34	0.32	0.312	0.306	0.303	0.301

 
（1）请估计：当摸球次数S很大时, 摸到白球的频率将会接近          ；
假如你去摸一次，你摸到红球的概率是           ；（精确到0.1）.
（2）试估算口袋中红球有多少只?

在元旦联欢会上，有一个开盒有奖的游戏，两只外观一样的盒子，一只装有奖品，一只
是空的，游戏规定：每人每次游戏时主持人先混合盒子再拿出来，参加游戏的同学随机打开其中一只，若
有奖品，就获得该奖品，若是空盒子，就表演一个节目．
（1）两个人参加游戏，都获奖的概率为_______．
（2）n个人参加游戏，全部获奖的概率为________．
（3）现取三只外观一样的盒子，一只内有奖品，另两只空盒子，游戏规则不变．两个人参加游戏，用画树形
图法求至少有一个人表演节目的概率．