初中数学利用频率估计概率填空题

我国魏晋时期数学家刘徽首创"割圆术"计算圆周率．随着时代发展，现在人们依据频率估计概率这一原理，常用随机模拟的方法对圆周率π进行估计．用计算机随机产生 m个有序数对（ x， y）（ x， y是实数，且0≤ x≤1，0≤ y≤1），它们对应的点在平面直角坐标系中全部在某一个正方形的边界及其内部．如果统计出这些点中到原点的距离小于或等于1的点有 n个，则据此可估计π的值为 　　．（用含 m， n的式子表示）

一个不透明的口袋里装有若干除颜色外其他完全相同的小球，其中有6个黄球，将口袋中的球摇匀，从中任意摸出一个球记下颜色后再放回，通过大量重复上述实验后发现，摸到黄球的频率稳定在30%，由此估计口袋中共有小球　　个．

公司以3元 $/\mathit{kg}$ 的成本价购进 $10000\mathit{kg}$ 柑橘，并希望出售这些柑橘能够获得12000元利润，在出售柑橘（去掉损坏的柑橘）时，需要先进行"柑橘损坏率"统计，再大约确定每千克柑橘的售价，如表是销售部通过随机取样，得到的"柑橘损坏率"统计表的一部分，由此可估计柑橘完好的概率为 　　（精确到 $0.1)$ ；从而可大约每千克柑橘的实际售价为 　　元时（精确到 $0.1)$ ，可获得12000元利润．

柑橘总质量     $n/\mathit{kg}$	损坏柑橘质量     $m/\mathit{kg}$	柑橘损坏的频率     $\frac{m}{n}$ （精确到     $0.001)$
$\dots$	$\dots$	$\dots$
250	24.75	0.099
300	30.93	0.103
350	35.12	0.100
450	44.54	0.099
500	50.62	0.101

大数据分析技术为打赢疫情防控阻击战发挥了重要作用．如图是小明同学的健康码（绿码）示意图，用黑白打印机打印于边长为 $2\mathit{cm}$ 的正方形区域内，为了估计图中黑色部分的总面积，在正方形区域内随机掷点，经过大量重复试验，发现点落入黑色部分的频率稳定在0.6左右，据此可以估计黑色部分的总面积约为 　 　 $c{m}^2$ ．

技术变革带来产品质量的提升．某企业技术变革后，抽检某一产品2020件，欣喜发现产品合格的频率已达到0.9911，依此我们可以估计该产品合格的概率为　　．（结果要求保留两位小数）

在“抛掷正六面体”的试验中，正六面体的六个面分别标有数字“1”“2”“3”“4”“5”“6”，在试验次数很大时，数字“6”朝上的频率的变化趋势接近的值是　　．

某射击运动员在同一条件下的射击成绩记录如下：

射击次数	20	40	100	200	400	1000
“射中9环以上”的次数	15	33	78	158	321	801
“射中9环以上”的频率 （结果保留小数点后两位）	0.75	0.83	0.78	0.79	0.80	0.80

根据频率的稳定性，估计这名运动员射击一次时“射中9环以上”的概率是　0.8　（结果保留小数点后一位）．

在一个不透明的袋中装有若干个材质、大小完全相同的红球，小明在袋中放入3个黑球（每个黑球除颜色外其余都与红球相同），摇匀后每次随机从袋中摸出一个球，记录颜色后放回袋中，通过大量重复摸球试验后发现，摸到红球的频率稳定在0.85左右，估计袋中红球有　　个．

在一个不透明的袋子中有若干个小球，这些球除颜色外无其他差别，从袋中随机摸出一球，记下其颜色，这称为一次摸球试验，然后把它重新放回袋中并摇匀，不断重复上述过程．以下是利用计算机模拟的摸球试验统计表：

摸球试验次数	100	1000	5000	10000	50000	100000
“摸出黑球”的次数	36	387	2019	4009	19970	40008
“摸出黑球”的频率（结果保留小数点后三位）	0.360	0.387	0.404	0.401	0.399	0.400

根据试验所得数据，估计“摸出黑球”的概率是　   ．（结果保留小数点后一位）

从甲地到乙地有，，三条不同的公交线路．为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况，在每条线路上随机选取了500个班次的公交车，收集了这些班次的公交车用时（单位：分钟）的数据，统计如下：

公交车用时 公交车用时的频数 线路					合计
	59	151	166	124	500
	50	50	122	278	500
	45	265	167	23	500

早高峰期间，乘坐　　（填“”，“ ”或“” 线路上的公交车，从甲地到乙地“用时不超过45分钟”的可能性最大．

林业部门要考察某种幼树在一定条件下的移植成活率，下表是这种幼树在移植过程中的一组数据：

移植的棵数 $n$	1000	1500	2500	4000	8000	15000	20000	30000
成活的棵数 $m$	865	1356	2220	3500	7056	13170	17580	26430
成活的频率 $\frac{m}{n}$	0.865	0.904	0.888	0.875	0.882	0.878	0.879	0.881

估计该种幼树在此条件下移植成活的概率为 　　．

若100个产品中有95个正品、5个次品，从中随机抽取一个，恰好是次品的概率是        ．

不透明的袋子中装有4个红球、3个黄球和5个蓝球，每个球除颜色不同外其它都相同，从中任意摸出一个球，则摸出        球的可能性最大．

一个口袋中有 16 个白球和若干个黑球，在不允许将球倒出来的前提下，为估计口袋中黑球的
个数，采用了如下的方法：从口袋中摸出 1 个球记下颜色放回摇匀，不断重复上述过程多次，发现 摸到黑球的频率稳定在 0.8，根据上述数据，可估计口袋中大约有    个黑球．

在一个不透明的布袋中装有2个白球和n个黄球，它们除颜色不同外，其余均相同，若从中随机摸出一个球，摸到黄球的概率是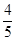，则n=。