初中数学利用频率估计概率试题

甲、乙两同学只有一张乒乓球比赛的门票，谁都想去，最后商定通过转盘游戏决定．游戏规则是：转动下面平均分成三个扇形且标有不同颜色的转盘，转盘连续转动两次，若指针前后所指颜色相同，则甲去；否则乙去．（如果指针恰好停在分割线上，那么重转一次，直到指针指向一种颜色为止）

（1）转盘连续转动两次，指针所指颜色共有几种情况？通过画树状图或列表法加以说明；
（2）你认为这个游戏公平吗？请说明理由．

现有5张正面分别标有数字0，1，2，3，4的不透明卡片，它们除数字不同外其余全部
相同。现将它们背面朝上，洗匀后从中任取一张，将该卡片上的数字记为，则使得关于的一元二次方程有实数根，且关于的分式方程有整数解的概率为         ．

在一个不透明的盒子中，装有4个黑球和若干个白球，它们除颜色外没有任何其他区别．摇匀后从中随机摸出一个球记下颜色，再把它放回盒子中．不断重复以上操作过程，共摸了100次球，发现有20次摸到黑球，据此估计盒子中白球的个数为（   ）

A．12个

B．16个

C．20个

D．30个

一个不透明的口袋中装有4个分别标有数字-1，-2，3，4的小球，它们的形状、大小完全相同．小红先从口袋中随机摸出一个小球记下数字为x；小颖在剩下的3个小球中随机摸出一个小球记下数字为y．
（1）小红摸出标有数字3的小球的概率是              ；
（2）请用列表法或画树状图的方法表示出由x，y确定的点P（x，y）所有可能的结果；
（3）若规定：点P （x，y）在第一象限或第三象限小红获胜；点P（x，y）在第二象限或第四象限则小颖获胜．请分别求出两人获胜的概率．

一个猜想是否正确，科学家们要经过反复的试验论证．下表是几位科学家“掷硬币”的实验数据：

实验者	德 $\cdot$摩根	蒲丰	费勒	皮尔逊	罗曼诺夫斯基
掷币次数	6140	4040	10000	36000	80640
出现“正面朝上”的次数	3109	2048	4979	18031	39699
频率	0.506	0.507	0.498	0.501	0.492

请根据以上数据，估计硬币出现“正面朝上”的概率为　　（精确到 $0.1)$．

如图，电路图上有四个开关A、B、C、D和一个小灯泡，闭合开关D或同时闭合开关A、B、C都可使小灯泡发光，则任意闭合其中两个开关，小灯泡发光的概率是（ ）

A．       B．         C．           D．

掷两枚质地均匀的骰子，两次出现的点数相同的概率是    ．

如图，为测量平地上一块不规则区域（图中的阴影部分）的面积，画一个边长为 $2m$的正方形，使不规则区域落在正方形内，现向正方形内随机投掷小石子（假设小石子落在正方形内每一点都是等可能的），经过大量重复投掷试验，发现小石子落在不规则区域的频率稳定在常数0.25附近，由此可估计不规则区域的面积是　   　 $m^2$．

在6张完全相同的卡片上分别画上线段、等边三角形、平行四边形、圆、正方形、直角梯形，在看不见图形的情况下随机摸出1张，这张卡片上的图形既是中心对称图形又是轴对称图形的概率是（  ）

A．

B．

C．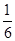

D．

一个不透明的袋中装有除颜色外均相同的8个黑球、4个白球和若干个红球．每次摇匀后随机摸出一个球，记下颜色后再放回袋中，通过大量重复摸球试验后，发现摸到红球的频率稳定于0.4，由此可估计袋中约有红球　　个．

在一个不透明的袋子中装有4个除颜色外完全相同的小球，其中白球1个，黄球1个，红球2个，摸出一个球不放回，再摸出一个球，两次都摸到红球的概率是（    ）

A．

B．

C．

D．

在阳光体育活动时间，小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球，当时只有一副空球桌，他们只能选两人打第一场．
（1）如果确定小亮打第一场，再从其余三人中随机选取一人打第一场，求恰好选中大刚的概率；
（2）如果确定小亮做裁判，用“手心、手背”的方法决定其余三人哪两人打第一场．游戏规则是：三人同时伸“手心、手背”中的一种手势，如果恰好有两人伸出的手势相同，那么这两人上场，否则重新开始，这三人伸出“手心”或“手背”都是随机的，请用画树状图的方法求小莹和小芳打第一场的概率．

扬州某毛绒玩具厂对一批毛绒玩具进行质量抽检的结果如下：

抽取的毛绒玩具数 $n$	20	50	100	200	500	1000	1500	2000
优等品的频数 $m$	19	47	91	184	462	921	1379	1846
优等品的频率 $\frac{m}{n}$	0.950	0.940	0.910	0.920	0.924	0.921	0.919	0.923

从这批玩具中，任意抽取的一个毛绒玩具是优等品的概率的估计值是　     　．（精确到 $0.01)$

一个布袋里有6只颜色不同的球，其中2个红球，4个白球，从布袋里任意摸出一个球，则摸出的球的红球的概率为（     ）

A．

B．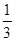

C．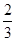

D．

表中记录了某种苹果树苗在一定条件下移植成活的情况：

移植的棵数 $n$	200	500	800	2000	12000
成活的棵数 $m$	187	446	730	1790	10836
成活的频率 $\frac{m}{n}$	0.935	0.892	0.913	0.895	0.903

由此估计这种苹果树苗移植成活的概率约为　　．（精确到 $0.1)$