初中数学利用频率估计概率试题

某种机器使用若干年后即被淘汰，该机器有一易损零件，为调查该易损零件的使用情况，随机抽取了100台已被淘汰的这种机器，经统计：每台机器在使用期内更换的该易损零件数均只有8，9，10，11这四种情况，并整理了这100台机器在使用期内更换的该易损零件数，绘制成如图所示不完整的条形统计图．

（1）请补全该条形统计图；

（2）某公司计划购买一台这种机器以及若干个该易损零件，用上述100台机器更换的该易损零件数的频率代替一台机器更换的该易损零件数发生的概率．

①求这台机器在使用期内共更换了9个该易损零件的概率；

②若在购买机器的同时购买该易损零件，则每个200元；若在使用过程中，因备用该易损零件不足，再购买，则每个500元．请你帮该公司用花在该易损零件上的费用的加权平均数进行决策：购买机器的同时应购买几个该易损零件，可使公司的花费最少？

下列说法错误的是 $($ 　　 $)$

A．	必然事件发生的概率为1
B．	平均数和方差都不易受极端值的影响
C．	抽样调查抽取的样本是否具有代表性，直接关系对总体估计的准确程度
D．	可以通过大量重复试验，用一个随机事件发生的频率去估计它的概率

为了解某地区九年级男生的身高情况，随机抽取了该地区100名九年级男生，他们的身高 $x\left(\mathit{cm}\right)$ 统计如下：

组别 $\left(\mathit{cm}\right)$	$x<160$	$160⩽x<170$	$170⩽x<180$	$x⩾180$
人数	5	38	42	15

根据以上结果，抽查该地区一名九年级男生，估计他的身高不低于 $180\mathit{cm}$ 的概率是 $($ 　　 $)$

A．

0.85

B．

0.57

C．

0.42

D．

0.15

某校为研究学生的课余爱好情况，采取抽样调查的方法，从阅读、运动、娱乐、上网等四个方面调查了若干学生的兴趣爱好，并将调查的结果绘制成如下两幅不完整的统计图，请你根据图中提供的信息解答下列问题：

（1）在这次研究中，一共调查了　　名学生；若该校共有1500名学生，估计全校爱好运动的学生共有　　名；

（2）补全条形统计图，并计算阅读部分圆心角是　　；

（3）在全校同学中随机选出一名学生参加演讲比赛，用频率估计概率，则选出的恰好是爱好阅读的学生概率是　　．

从甲地到乙地有，，三条不同的公交线路．为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况，在每条线路上随机选取了500个班次的公交车，收集了这些班次的公交车用时（单位：分钟）的数据，统计如下：

公交车用时 公交车用时的频数 线路					合计
	59	151	166	124	500
	50	50	122	278	500
	45	265	167	23	500

早高峰期间，乘坐　　（填“”，“ ”或“” 线路上的公交车，从甲地到乙地“用时不超过45分钟”的可能性最大．

如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果．

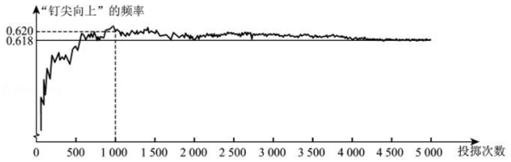
下面有三个推断：

①当投掷次数是500时，计算机记录"钉尖向上"的次数是308，所以"钉尖向上"的概率是0.616；

②随着试验次数的增加，"钉尖向上"的频率总在0.618附近摆动，显示出一定的稳定性，可以估计"钉尖向上"的概率是0.618；

③若再次用计算机模拟此实验，则当投掷次数为1000时，"钉尖向上"的频率一定是0.620．

其中合理的是 $($ 　　 $)$

A．

①

B．

②

C．

①②

D．

①③

林业部门要考察某种幼树在一定条件下的移植成活率，下表是这种幼树在移植过程中的一组数据：

移植的棵数 $n$	1000	1500	2500	4000	8000	15000	20000	30000
成活的棵数 $m$	865	1356	2220	3500	7056	13170	17580	26430
成活的频率 $\frac{m}{n}$	0.865	0.904	0.888	0.875	0.882	0.878	0.879	0.881

估计该种幼树在此条件下移植成活的概率为 　　．

在一个不透明的盒子中，共有“一白三黑”个围棋子，它们除了颜色之外没有其它区别．
（1）随机地从盒中提出子，则提出白子的概率是多少？
（2）随机地从盒中提出子，不放回再提第二子．请你用画树状图或列表的方法表示所有等可能的结果，并求恰好提出“一黑一白”子的概率．

在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共5只，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复．下表是活动进行中的一组统计数据：

摸球的次数n	100	150	200	500	800	1000
摸到白球的次数m	58	96	116	295	484	601
摸到白球的频率	0.58	0.64	0.58	0.59	0.605	0.601

 
（1）请估计：当n很大时，摸到白球的频率将会接近      ；（精确到0.1）
（2）试估算口袋中白种颜色的球有多少只？
（3）请画树状图或列表计算：从中先摸出一球，不放回，再摸出一球；这两只球颜色不同的概率是多少？

地球上陆地与海洋面积的比是3：7，宇宙中一块陨石进入地球，落在陆地的概率是（ ）

A．

B．

C．

D．

从分别标有1、2、3、4的四张卡片中，一次同时抽2张，其中和为奇数的概率是             ．

2015年国家实施“全面二孩政策”，人民医院迎来人口出生小高峰，某天出生了3个婴儿，假设生男生女的机会相同，那么这3个婴儿中，出现1个男婴、2个女婴的概率是多少？画出树状图或列表．

在﹣1，0，，1，，中任取一个数，取到无理数的概率是       ．

给甲乙丙三人打电话，若打电话的顺序是任意的，则第一个打电话给甲的概率为（ ）

A．

B．

C．

D．

初三年级组织冬季拔河比赛，先用抽签的方法两两一组进行初赛，初三年级共有（1）（2）（3）（4）四个班，小明是初三（1）班的学生，他说“我们班和初三（2）班恰好分在同一组的概率是”你认为正确吗？如果正确，说明理由；如果不正确，写出正确的解答过程．