初中数学对称式和轮换对称式选择题

如图，两个边长相等的正方形ABCD和EFGH，正方形EFGH的顶点E固定在正方形ABCD的对称中心位置，正方形EFGH绕点E顺时针方向旋转，设它们重叠部分的面积为S，旋转的角度为θ，S与θ的函数关系的大致图象是（　　）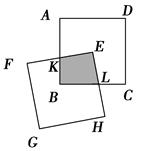

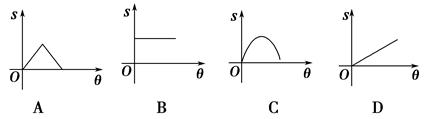
如图，在平面直角坐标系中，点A的坐标为（0，3），△OAB沿x轴向右平移后得到△O′A′B′，点A的对应点在直线y=x上一点，则点B与其对应点B′间的距离为（）

A．

B．3

C．4

D．5

如图，正方形ABCD的边长是3cm，一个边长为1cm的小正方形沿着正方形ABCD的边AB→BC→CD→DA→AB连续地翻转，那么这个小正方形第一次回到起始位置时，它的方向是( )


A. B. C. D.

如图的坐标平面上有一正五边形ABCDE，其中C、D两点坐标分别为（1，0）、（2，0）．若在没有滑动的情况下，将此正五边形沿着x轴向右滚动，则滚动过程中，下列哪个点会经过点（76，0）？（）

A．A B．B C．C D．D

下列图形中，是轴对称而不是中心对称图形的是（　　）

A．平行四边形

B．菱形

C．等腰梯形

D．直角梯形

如图，把抛物线y=x²与直线y=1围成的图形OABC绕原点O顺时针旋转90°后，再沿x轴向右平移1个单位得到图形O₁A₁B₁C₁，则下列结论错误的是（）

A．点O1的坐标是（1，0）

B．点C1的坐标是（2，﹣1）

C．四边形OBA1B1是矩形

D．若连接OC，则梯形OCA1B1的面积是3

点（－2，3）关于原点对称的点的坐标是

A．(2,3)

B．(－2,－3)

C．(2,－3)

D．(－3,2)

把抛物线y=2－4x－5绕顶点旋转180º，得到的新抛物线的解析式是（）

A．y= -2－4x－5	B．y=-2+4x+5
C．y=－2+4x－9	D．以上都不对

（11·佛山）一个图形无论经过平移还是旋转，有以下说法（）
①对应线段平行；②对应线段相等；
③对应角相等；④图形的形状和大小都没有发生变化

A．①②③

B．①②④

C．①③4

D．②③④

如图，在平面直角坐标系中，A(1,0)，B(0,3)，以AB为边在第一象限作正方形ABCD,点D在双曲线y=(k≠0)上，将正方形沿x轴负方向平移 m个单位长度后，点C恰好落在双曲线上，则m的值是（）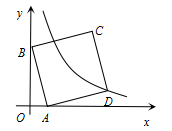

A．2

B．3

C．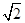

D．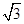

如图，在Rt△ABC中，∠BAC=90°，∠B=60°，△AB′C′可以由△ABC绕点A顺时针旋转90°得到（点B′与点B是对应点，点C′与点C是对应点），连接CC′，则∠CC′B′的度数是（）

A．45°

B．30°

C．25°

D．15°

如图，半径为3的⊙P在第一象限，动点A沿着⊙P运动一周，在点A运动的同时，作点A关于原点O的对称点B，再以AB为边作等边△ABC，点C在第二象限，点C 随点A运动所形成的图形的面积为（）

A．

B．

C．

D．

如图，在△ABC中，AB=AC，BC=24，tanC=2，如果将△ABC沿直线l翻折后，点B落在边AC的中点E处，直线l与边BC交于点D，那么BD的长为（）

A．13

B．

C．

D．12

如图，动点P从点A出发，沿线段AB运动至点B后，立即按原路返回，点P在运动过程中速度不变，则以点B为圆心，线段BP长为半径的圆的面积S与点P的运动时间t的函数图象大致为（ ）

在下列图形中，既是轴对称图形，又是中心对称图形的是（　　）