为庆祝第29届北京奥运圣火在泉州站传递，甲、乙两校联合准备文艺汇演．甲、乙两校共92人（其中甲校人数多于乙校人数，且甲校人数不够90人）准备统一购买服装（一人买一套）参加演出，下面是服装厂给出的演出服装的价格表：
| 购买服装的套数 |
1套至45套 |
46套至90套 |
91套及以上 |
| 每套服装的价格 |
60元 |
50元 |
40元 |
如果两所学校分别单独购买服装，一共应付5000元．
（1）如果甲、乙两校联合起来购买服装，那么比各自购买服装共可以节省多少钱？
（2）甲、乙两校各有多少学生准备参加演出？
（3）如果甲校有9名同学抽调去参加迎奥运书法比赛不能参加演出，那么你有几种购买方案，通过比较，你该如何购买服装才能最省钱？
定义一种新运算“⊕”：a⊕b=a-2b，比如：2⊕（-3）=2-2×（-3）=2+6=8．
（1）求（-3）⊕2的值；
（2）若（x-3）⊕（x+1）=1，求x的值．
如图，若点A在数轴上对应的数为
，点B在数轴上对应的数为b，且，b满足
（1）求线段AB的长；
（2）点C在数轴上对应的数为x，且x是方程
的解，在数轴上是否存在点P，使得PA+PB=PC？若存在，求出点P对应的数；若不存在，说明理由；
（3）在（1）（2）条件下，点A，B，C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒4个单位长度和9个单位长度的速度向右运动，假设t秒钟过后，若点B与点C之间的距离表示为BC，点A与点B之间的距离表示为AB，请问：AB﹣BC的值是否随时间t的变化而改变？若变化，请说明理由；若不变，请求其常数值．
定义新运算：对于任意有理数a，b，都有a※b=a（a﹣b）+1，等式右边是通常的加法，减法及乘法运算，比如：2※5=2×（2﹣5）+1=2×（﹣3）+1=﹣6+1=﹣5．
（1）求（﹣2）※3的值；
（2）若3※x=5※（x﹣1），求x的值．
修筑一条公路，甲工程队单独承包要80天完成，乙工程队单独承包要120天完成。
（1）现由甲、乙两个工程队合作承包，多少天可以完成？
（2）如果甲、乙两工程队合作了30天后，因甲工程队另有任务，剩下的工作由乙工程队完成，则修好这条公路一共需要多少天完成？
甲、乙两个旅行团同时去苏州旅游，已知乙团人数比甲团人数多4人，两团人数之和恰等于两团人数之差的18倍．
（1）问甲、乙两个旅行团的人数各是多少？
（2）若乙团中儿童人数恰为甲团人数的3倍少2人，某景点成人票价为每张100元，儿童票价是成人票价的六折，两旅行团在此景点所花费的门票费用相同，求甲、乙两团儿童人数各是多少？
下面是解分式方程的过程，阅读完后请填空：
解方程：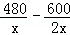
=45．
解：方程两边都乘以2x，得960﹣600=90x，
解这个方程，得x=4．
经检验，x=4是原方程的根．
第一步计算中的2x是： ；这个步骤用到的依据是 ；
解分式方程与解一元一次方程之间的联系是： ．
（本题12分） 请根据图中提供的信息,回答下列问题:
（1）一个水瓶与一个水杯分别是多少元?
（2）甲、乙两家商场同时出售同样的水瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定：这两种商品都打八折；乙商场规定：买一个水瓶赠送两个水杯，另外购买的水杯按原价卖．若某单位想要买5个水瓶和20个水杯，请问选择哪家商场购买更合算，并说明理由.（必须在同一家购买）
（本题10分）“十一”节，朱老师驾车从江都出发，上高速公路途经江阴大桥到上海下高速，其间用了4．5小时；返回时平均速度提高了10千米／时，比去时少用了半小时回到江都．
（1）根据题意，甲、乙两名同学分别列出尚不完整的方程如下：
甲：
乙：
根据甲、乙两名同学所列的方程，请你分别指出未知数
表示的意义，然后在方框中补全两位同学所列的方程：
甲：
表示______ __ ____；乙：
表示______ ______；甲所列方程中的方框内该
填 ；乙所列方程中的第一个方框内该填 ，第二个方框内该填 ．
（2）求江都与上海两地间的高速公路路程．（写出完整的解答过程）
春节将至，某移动公司计划推出两种新的计费方式，如下表所示：
| |
方式1 |
方式2 |
| 月租费 |
30元/月 |
0 |
| 本地通话费 |
0．20元/分钟 |
0．40元/分钟 |
请解决以下两个问题：（通话时间为正整数）
（1）若本地通话100分钟，按方式一需交费多少元？按方式二需交费多少元？
（2）对于某月本地通话，当通话多长时间时，按两种计费方式的收费一样多？
试题篮
()
粤公网安备 44130202000953号
．
的解与方程
的解相同，求式子
的值 ．
