已知购买1个足球和1个篮球共需130元,购买2个足球和1个篮球共需180元.
(1)求每个足球和每个篮球的售价;
(2)如果某校计划购买这两种球共54个,总费用不超过4000元,问最多可买多少个篮球?
计算
(1)解不等式:5(x﹣2)﹣2(x+1)>3.
(2)解不等式 ≤
≤ ,并求出它的非负整数解。
,并求出它的非负整数解。
下列不等式变形正确的是( )
| A.由a>b得ac>bc | B.由a>b得﹣2a>﹣2b |
| C.由a>b得﹣a<﹣b | D.由a>b得a﹣2<b﹣2 |
已知a,b为实数,则解可以为 – 2 < x < 2的不等式组是( )
A. |
B.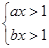 |
C. |
D. |
不等式9-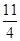 x>x+
x>x+ 的正整数解的个数是 ( )
的正整数解的个数是 ( )
| A.1 | B.2 | C.3 | D.4 |
随着人民生活水平的不断提高,大丰区家庭轿车的拥有量逐年增加.据统计,怡景小区2012年底拥有家庭轿车144辆,2014年底家庭轿车的拥有量达到196辆.2014年底小区拥有室内车位和露天车位共180个.假设该小区2012年底到2016年底家庭轿车拥有量的年平均增长率都相同.
(1)估计该小区到2015年底家庭轿车将达到多少辆?(结果四舍五入取整数)
(2)为了缓解停车矛盾,该小区决定投资25万元再建造若干个停车位.据测算,建造费用分别为室内车位6000元/个,露天车位2000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的3倍,但不超过室内车位的4.5倍.在投资款恰好用完的情况下求该小区可建两种车位各多少个?试写出所有可能的方案.并判断有没有方案能够满足2016年底小区所有轿车同时停车的需求?
兰新铁路的通车,圆了全国人民的一个梦,坐上火车去观赏青海门源百里油菜花海,感受大美青海独特的高原风光,暑假某校准备组织学生、老师到门源进行社会实践,为了便于管理,师生必须乘坐在同一列高铁上,根据报名人数,若都买一等座单程火车票需2340元,若都买二等座单程火车票花钱最少,则需1650元:
西宁到门源的火车票价格如下表
| 运行区间 |
票价 |
|
|
| 上车站 |
下车站 |
一等座 |
二等座 |
| 西宁 |
门源 |
36元 |
30元 |
(1)参加社会实践的学生、老师各有多少人?
(2)由于各种原因,二等座火车票单程只能买x张(参加社会实践的学生人数<x<参加社会实践的总人数),其余的须买一等座火车票,在保证每位参与人员都有座位坐并且总费用最低的前提下,请你写出购买火车票的总费用(单程)y与x之间的函数关系式.

某糕饼店主贷款2.2万元购进一台机器,生产蛋黄酥.已知产品的成本是每个5元,售价是每个8元,应付的税款和其他费用的和是售价的10%.若每个月能生产并销售2000个蛋黄酥.
(1)问每个月所获得利润为多少元?
(2)问至少几个月后能赚回这台机器的贷款?
(1)解不等式:2(x+1)﹣1≥3x+2,并把解集表示在数轴上.
(2)解不等式组 ,并写出不等式组的整数解.
,并写出不等式组的整数解.
一次知识竞答比赛,共16道选择题,评选办法是:答对一道题得6分,答错一道题倒扣2分,不答则不扣分,王同学全部做答,如果王同学想成绩在60分以上,试写出他答对x题应满足的不等式 .
试题篮
()