“保护好环境,拒绝冒黑烟”.某市公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2) 预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
某校七年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如下图表:

请你根据以上信息,解答下列问题:
(1)写出a,b,d的值并补全条形图;
(2)请你估计该校七年级共有多少名学生本次成绩不低于80分.
商店为了对某种商品促销,将定价为3元的商品,以下列方式优惠销售:若购买不超过5件,按原价付款;若一次性购买5件以上,超过部分打八折.现有26元钱,最多可以购买该商品 件.
解不等式组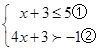 请结合题意填空,完成本题的解答:
请结合题意填空,完成本题的解答:
(1)解不等式①,得 ;
(2)解不等式②,得 ;
(3)把不等式①和②的解集在数轴上表示出来: .
(4)原不等式组的解集为 .
乐乐和欢欢同学同时去上学,从家到学校的距离都是2km,他们走路的速度为6km/h,跑步的速度为10km/h.请根据以上信息,提出一个可以用一元一次不等式解决的问题,并给出解决办法.
(满分8分)某校运动会需购买A、B两种奖品.若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)求A、B两种奖品单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍.设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式,求出自变量m的取值范围,并确定最少费用W的值.
在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
目前节能灯在城市已基本普及,今年山东省面向县级及农村地区推广,为响应号召,某商场计划购进甲,乙两种节能灯共1200只,这两种节能灯的进价、售价如下表:
| 类型 |
进价(元/只) |
售价(元/只) |
| 甲型 |
25 |
30 |
| 乙型 |
45 |
60 |
(1)如何进货,进货款恰好为46000元?
(2)如何进货,商场销售完节能灯时获利最多且不超过进货价的30%,此时利润为多少元?
试题篮
()