初中数学含绝对值的一元一次不等式试题

（1）解不等式7x-3≤9x+2，并把解表示在数轴上；
（2）解不等式组：，并写出该不等式组的整数解．

（1）先化简，再求值：（x+3）（x﹣3）﹣x（x﹣2），其中x=4．
（2）解不等式组，并把解集在数轴上表示出来．

某商店销售10台A型和20台B型电脑的利润为4000元，销售20台A型和10台B型电脑的利润为3500元．
（1）求每台A型电脑和B型电脑的销售利润；
（2）该商店计划一次购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的2倍，设购进A型电脑x台，这100台电脑的销售总利润为y元．
①求y关于x的函数关系式；
②该商店购进A型、B型电脑各多少台，才能使销售总利润最大？
（3）实际进货时，厂家对A型电脑出厂价下调m（0＜m＜100）元，且限定商店最多购进A型电脑70台，若商店保持同种电脑的售价不变，请你根据以上信息及（2）中条件，设计出使这100台电脑销售总利润最大的进货方案．

若关于x的不等式整数解共有2个，则m的取值范围是（   ）

A．3＜m＜4

B．3＜m≤4

C．3≤m≤4

D．3≤m＜4

下列各数中，为不等式组的解的是（ ）

A．-1

B．2

C．0

D．4

先化简，再选择一个你喜欢的整数代入求值：，
其中a满足．

若不等式x＜a只有5个正整数解，则a的取值范围      ．

关于x的不等式组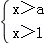的解集为x＞1，则a的取值范围是（ ）

A．a≥1

B．a＞1

C．a≤1

D．a＜1

不等式组的解集是             ．

商店为了对某种商品促销，将定价为3元的商品，以下列方式优惠销售：若购买不超过5件，按原价付款；若一次性购买5件以上，超过部分打八折，现有27元钱，最多可以购买该商品多少件？

（1997•河北）由x＜y得到ax＞ay的条件是（ ）

A．a≥0

B．a≤0

C．a＞0

D．a＜0

解不等式组．

若a＞b，则下列式子正确的是（ ）

A．-2015a＞-2015b	B．a＜0.5b
C．2015-a＞2015-b	D．a-2015＞b-2015

学校计划选购甲、乙两种图书作为“校园读书节”的奖品．已知甲图书的单价是乙图书单价的1.5倍；用600元单独购买甲种图书比单独购买乙种图书要少10本．
（1）甲、乙两种图书的单价分别为多少元？
（2）若学校计划购买这两种图书共40本，且投入的经费不超过1050元，要使购买的甲种图书数量 不少于乙种图书的数量，则共有几种购买方案？

把不等式组的解集在数轴上表示正确的是（   ）