如图， 一艘轮船由海平面上A地出发向南偏西40º的方向行驶40海里到达B地，再由B地向北偏西20º的方向行驶40海里到达C地，则A、C两地相距（ ）
| A．40海里 | B．30海里 |
| C．50海里 | D．60海里 |
2010年广州亚运会吉祥物取名“乐羊羊”．图中各图是按照一定规律排列的羊的组图，图
有1只羊，图
有3只羊，……，则图⑩有（ ）只羊． 
| A．53 | B．54 | C．55 | D．56 |
古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”，而把1、4、9、16 … 这样的数称为“正方形数”．从图7中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中，符合这一规律的是（ ）
| A．13 =" 3+10" | B．25 =" 9+16" |
| C．36 =" 15+21" | D．49 = 18+31 |
小亮的父亲想购买同一种大小一样、形状相同的地板砖铺设地面，小亮根据所学知识告诉父亲，为了能够做到无缝隙、不重叠地铺设，购买的地板砖形状不能是（ ）
| A．正三角形 | B．正方形 | C．正五边形 | D．正六边形 |
如图是一个由正方形ABCD和半圆O组成的封闭图形，点O是圆心．点P从点A出发，沿线段AB、弧BC和线段CD匀速运动，到达终点D．运动过程中OP扫过的面积（s）随时间（t）变化的图象大致是 
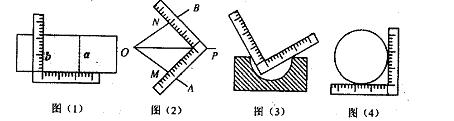
用一把带有刻度的直尺，① 可以画出两条平行的直线
与b，如图⑴；② 可以画出∠AOB的平分线OP，如图⑵所示；③ 可以检验工件的凹面是否为半圆，如图⑶所示；④ 可以量出一个圆的半径，如图⑷所示．这四种说法正确的个数有
| A．1个 | B．2个 | C．3个 | D．4个 |
为了美化城市，建设中的某休闲中心准备用边长相等的正方形和正八边形两种地砖镶嵌地面，在每一个顶点周围，正方形、正八边形地砖的块数分别是（ ）
| A． 1、2 | B． 2、1 | C． 2、3 | D． 3、2 |
【原创】在俄罗斯民间流着这样一道数学趣题：甲、乙两人合养了若干头羊，而每头羊的卖价又恰与羊的头数相等，全部卖完后，两人按下面的方法分钱：先由甲拿十元，再由乙拿十元，如此轮流，拿到最后，剩下不足十元，轮到乙拿去。为了平均分配，甲应该找补给乙多少元？（ ）
| A．1元 | B．2元 | C．3元 | D．4元 |
【改编】观察下列图形及图形所对应的算式，根据你发现的规律计算1+8+16+24+……+8n（n是正整数）的结果为
A． |
B． |
C． |
D． |
如图，四个电子宠物排座位：一开始，小鼠、小猴、小兔、小猫分别坐在1、2、3、4号的座位上，以后它们不停地交换位置，第一次上下两排交换位置，第二次是在第一次交换位置后，再左右两列交换位置，第三次是在第二次交换位置后，再上下两排交换位置，第四次是在第三次交换位置后，再左右两列交换位置，…，这样一直继续交换位置，第2008次交换位置后，小鼠所在的座号是（ ）.
| A．1 | B．2 | C．3 | D．4 |
某工厂第二季度的产值比第一季度的产值增长了
，第三季度的产值又比第二
季度的产值增长了，则第三季度的产值比第一季度增长了 （ ）
A． |
B． |
C． |
D． |
如图，将矩形纸片ABCD（图1）按如下步骤操作：（1）以过点A的直线为折痕
折叠纸片，使点B恰好落在AD边上，折痕与BC边交于点E（如图2）；（2）以过点E的
直线为折痕折叠纸片，使点A落在BC边上，折痕EF交AD边于点F（如图3）；（3）将纸
片收展平，那么∠AFE的度数为 （ ）
| A．60° | B．67.5° | C．72° | D．75° |
对点（x，y ）的一次操作变换记为P 1（x，y ），定义其变换法则
如下：P 1（x，y ）=（ 
， 
）；且规定 
（ 
为大于1的整数）．如
P 1（1，2 ）=（3， 
），P 2（1，2 ）= P 1（P 1（1，2 ））= P 1（3， ）=（2，4），P 3（1，
2 ）= P 1（P 2（1，2 ））= P 1（2，4）=（6， 
）．则P 2011（1， ）=（ ）
| A． | （0,2 1005） | B． | （0,-2 1005） | C． | （0,-2 1006） | D． | （0,2 1006） |
试题篮
()
粤公网安备 44130202000953号
五个景点之间的路线如图所示．若每条路线的里程
及行驶的平均速度
用
表示，则从景点
到景点
用时最少的路线是
元（不足1分钟按1分钟计）．某天小芳给同学打了一个6分钟的市 
元；小刚现准备给同学打市电话6分钟，他经过思考以后，决定先打 
元．如果你想给某同学打市话，准备通话 
元 
元 
元 
元 